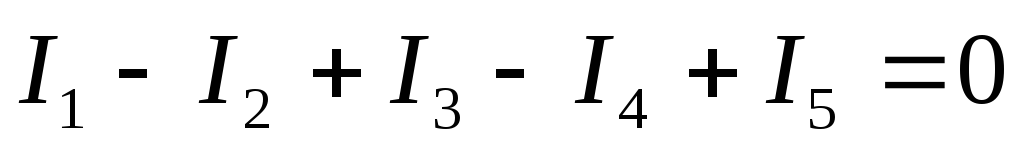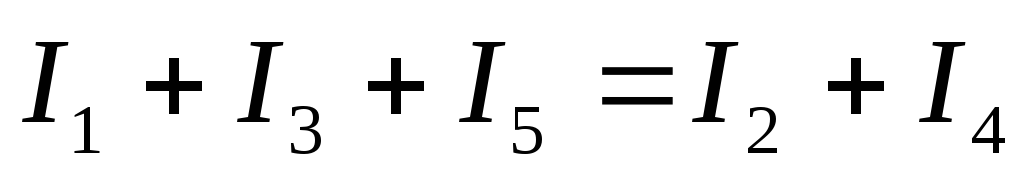Правила КирхгофаOh no, theres been an error

Закон Кирхгофа страница 1

Основы > Задачи и ответы > Постоянный электрический ток

Закон Кирхгофа (страница 1)
Применение закона Кирхгофа к расчету линейных электрических цепей постоянного тока

1. В цепи (рисунок 10) известны значения токов ; величины сопротивлений 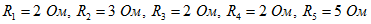. Определить напряжение U на входных зажимах цепи, сопротивление и величину Е источника ЭДС.Решение:
По закону Ома определим напряжение между узлами 3-2:
Из уравнения, составленного по первому закону Кирхгофа для узла 3:
определим ток
Тогда, по закону Ома для ветви с сопротивлением
откуда выражаем величину Е источника ЭДС:
Напряжение можно выразить из уравнения, записанного по II закону Кирхгофа для контура 1-3-2-1: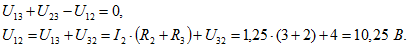
Зная величины напряжения и тока , определим величину сопротивления
Напряжение на входных зажимах цепи определится:
Ток определим из уравнения, записанного по первому закону Кирхгофа для 1 узла: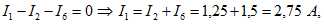
тогда2. В цепи (рисунок 11) известны величины сопротивлений резистивных элементов ; мощность, изменяемая ваттметром Р=320 Вт. Определить токи ветвей, напряжение на зажимах цепи.Решение:
Из формулы для расчета мощности выражаем ток
Затем определяем напряжение на зажимах параллельных ветвей:
По закону Ома определяем ток в ветви с сопротивлением
Значение тока в неразветвленной части цепи определим из уравнения, записанного по первому закону Кирхгофа для узла 1:
Напряжение на входных зажимах цепи можно представить как сумму падений напряжений на сопротивлениях
где
тогда

3. На рисунке 12 показана часть сложной цепи. Задано: 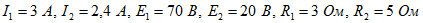. Найти напряжение .Решение:
Уравнение по второму закону Кирхгофа для данного контура, при выбранном направлении обхода контура, запишется следующим образом:
откуда выражаем напряжение 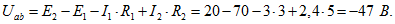4. В схеме (рисунок 13) известны: 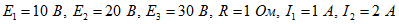. Определить напряжения .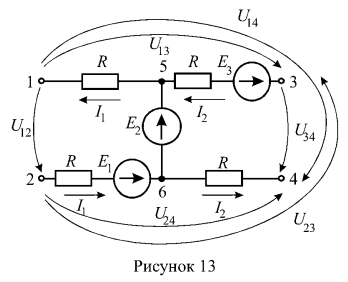Решение:
Считаем направления обходов контуров совпадающими с направлениям искомых напряжений. Запишем уравнения по второму закону Кирхгофа для каждого контура и выразим напряжения:контур 1-2-6-5-1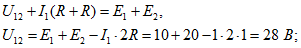
контур 3-4-6-5-3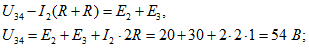
контур 1-3-5-1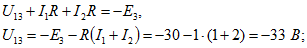
контур 2-4-6-2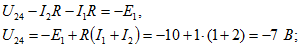
контур 1-4-6-5-1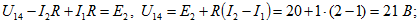
контур 2-3-5-6-2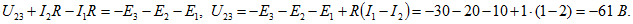5. Определить показание амперметра (рисунок 14), если 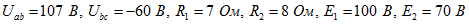.Решение:
По закону Ома определим значения токов в ветвях:
Запишем уравнение по первому закону Кирхгофа для узла b:
откуда6. На рисунке 15 показана часть сложной цепи. Найти напряжения , если 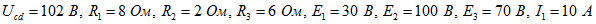.Решение:
По закону Ома определим ток на участке с-d:
Запишем уравнение по второму закону Кирхгофа для контура a-b-c-d:
откуда выразим напряжение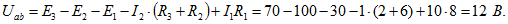

7. В схеме электрической цепи, приведенной на рисунке 16, определить токи в ветвях пользуясь законами Кирхгофа. Параметры элементов цени: 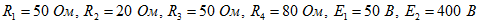.Решение:
Выбираем произвольно положительные направления искомых токов ветвей и обозначаем их на схеме. Составляем уравнение по первому закону Кирхгофа для узла 1. Выбрав направления обходов контуров, составляем уравнения по второму закону Кирхгофа. Получаем систему из трех уравнений:
Решаем полученную систему уравнений с помощью определителей: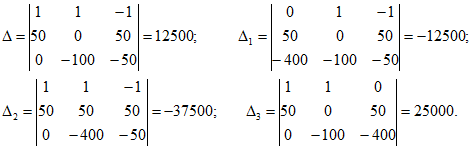
Находим значения токов: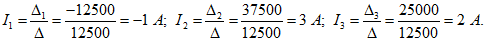
Для проверки правильности расчета составим уравнение баланса мощностей:
Мощность источников: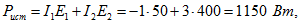
Мощность потребителей: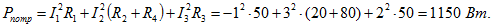8. Определить токи ветвей цепи (рисунок 17), если: .Решение:
Произвольно задаемся положительными направлениями токов в ветвях с сопротивлениями . В ветви с источником тока направление тока уже определено полярностью источника. Составляем уравнение по первому закону Кирхгофа для узла 1. Количество контурных уравнений зависит от количества ветвей с неизвестными токами, т.е. ветвей, не содержащих источники тока. Для данной цепи количество контурных уравнений равно 1. Составим систему уравнений: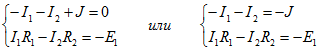
Решаем систему уравнений с помощью определителей: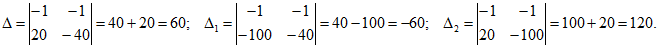
Определяем значения токов:

Смотри полное содержание по представленным решенным задачам на websor.

Первый закон Кирхгофа

На рисунке 5 показан электрический узел,
в котором сходятся n= 5
ветвей с токами, часть из которых
направлены к узлу, а часть – от него.

Первый закон Кирхгофав первой
редакции читается следующим образом:алгебраическая сумма токовв
узле равна нулю, то есть

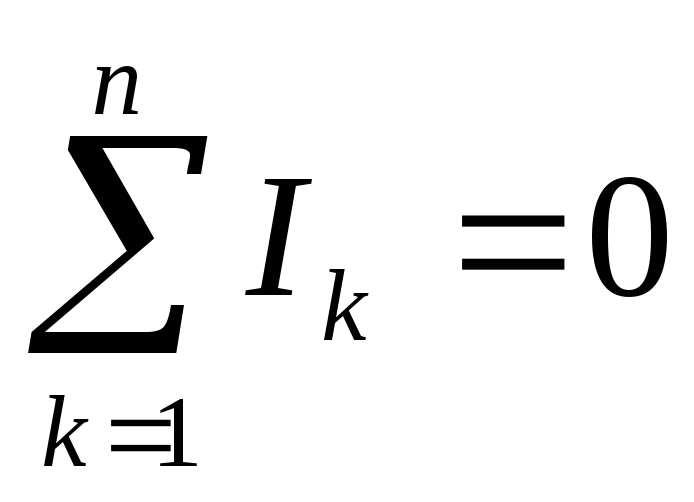
(8)

.

Вуравнении (8) токи, направленные к узлу,
подставляют обычно со знаком «+», а от
узла – со знаком «»
(можно и наоборот).

Применительно к узлу, показанному на
рисунке 5, равенство (8) записывается в
свернутом виде:

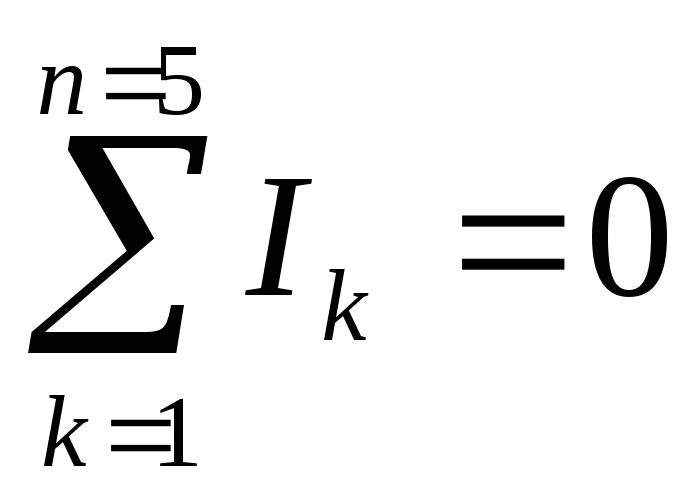
или в развернутом:

.

Е

(9)

сли перенести в последнем равенстве
отрицательные токи в правую часть, то
получим:

.

Из равенства (9) вытекает вторая редакция
первого закона Кирхгофа:

Сумма токов, входящих в узел, равна
сумме токов, выходящих из узла.

Справедливость первого закона Кирхгофа
можно подтвердить рассуждением «от
противного». Если предположить, что в
узел в каждый момент времени притекает
больше зарядов, чем вытекает (или
наоборот), то электрические потенциалы
узлов все время будут изменяться, а,
следовательно, будет изменяться и
распределение токов в элементах схемы,
что практически не наблюдается и
противоречит здравому смыслу.