Что такое разность потенциалов
Содержание:
Выражение для потенциала поля точечного заряда
Пусть положительный заряд находится на расстоянии от положительного заряда (см. рис. 3).
Рис. 3. Изначальное положение заряда
Какую работу совершит электрическое поле при перемещении заряда вдоль радиуса в точку, отдаленную на от ? (См. рис. 4.)
Рис. 4. Конечное положение заряда
По определению работа силы равна этой силе, умноженной на перемещение:
В данном случае действует сила электрического взаимодействия (см. рис. 5), по закону Кулона .
Рис. 5. Действие силы электрического взаимодействия
Сила и перемещение в нашем случае сонаправлены, и . Так мы можем находить работу для случая, когда сила постоянна на всей траектории. Здесь же сила изменяется по мере отдаления зарядов друг от друга.
Обозначим перемещение заряда (см. рис. 6).
Рис. 6. Перемещение заряда
По мере перемещения заряда сила изменяется, но на малом (в сравнении с расстоянием до заряда ) отрезке можем считать ее постоянной и находить работу по определению, которое мы привели выше.
Работа, совершаемая силой Кулона на таком малом отрезке равна , где силу можно считать постоянной на всем отрезке . Тогда работа при перемещении на расстояние будет равна сумме работ на участках (), на каждом из которых сила Кулона постоянна и равна .
Эта сумма будет равна
Подробный вывод этой формулы вы можете проследить в ответвлении.
Работа при перемещении электрического заряда
Работа по перемещению заряда на малом участке равна:
Работа на участке равна сумме работ на каждом участке :
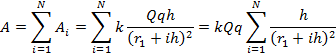
Воспользуемся приближенным равенством:
Прежде чем его применить, покажем, что равенство справедливо. Приведем правую часть к общему знаменателю:
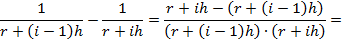
Раскроем скобки:
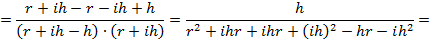
Заметим, что – пренебрежимо малая по сравнению с величина, не может считаться пренебрежимо малой, т. к. количество участков велико. Поэтому в знаменателе можем пренебречь членами и .
Вернемся к нахождению работы. Распишем выражение по полученной формуле:
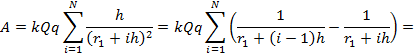
Распишем сумму:
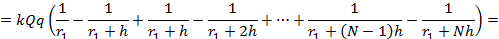
Мы знаем, что работа связана с энергией. Система обладает энергией, если силы, возникающие в системе, могут выполнить работу (в нашем случае это сила электростатического взаимодействия зарядов). Работа равна уменьшению потенциальной энергии:
Сравнив с выражением , делаем вывод, что – это потенциальная энергия взаимодействия двух зарядов. Ранее мы приняли, что потенциальная энергия заряда, отдаленного от источника электрического поля на бесконечность, равна нулю. Посмотрим, как с этим согласуется полученная формула:
Действительно, будет равна нулю на бесконечном отдалении от заряда , т. к. при .
Теперь проверим, как полученный результат соотносится с моделью, в которой разноименные заряды обозначены знаками плюс и минус. Если заряды одноименные, то потенциальная энергия взаимодействия положительна . Система стремится к состоянию с наименьшей потенциальной энергией (как и, например, камень на некоторой высоте над поверхностью земли, предоставленный сам себе, будет падать вниз, т. е. уменьшать высоту и с ней потенциальную энергию )
Действительно, заряды будут отталкиваться и сила электрического взаимодействия будет вызывать перемещение заряда на большее расстояние, потенциальная энергия будет уменьшаться.
Если заряды разноименные, то потенциальная энергия взаимодействия имеет знак минус. Заряды притягиваются, и сила их взаимодействия вызывает перемещение заряда на меньшее расстояние , потенциальная энергия уменьшается.
Напряженность электрического поля
Напряженность ЭП — характеристика векторная, определяемая в каждой точке и величиной, и направлением. Если в ЭП поместить малый положительный заряд, который своим присутствием не вызовет заметного перераспределения зарядов на телах, создающих поле, то отношение силы, действующей на заряд, к величине заряда Q определяет напряженность поля в данной точке:
Таким образом, Е — силовая характеристика ЭП, определяемая при условии, что внесенный в данную точку поля заряд не исказил поля, существовавшего до его внесения. Отсюда следует, что сила /, действующая на точечный заряд Q, внесенный в поле, будет равна
где Ё — напряженность ЭП в точке расположения заряда, а напряженность численно равна силе, действующей на единичный заряд.
Если использовать закон Кулона, который является исторически первым законом из области электромагнитных явлений и определяет силу / взаимодействия двух точечных электрических зарядов Q и Q2, то сила, действующая по прямой х, соединяющей эти заряды, будет равна
где с — абсолютная диэлектрическая проницаемость среды, то модуль напряженности Е в поле точечного заряда можно определить в виде
Рис. 9.1. Картина ЭП
Поскольку сила, действующая на электрический заряд со стороны ЭП, имеет вполне определенное направление, приходится говорить о направленности свойств этого поля. При этом за направление ЭП в данной точке пространства принимают направление вектора напряженности поля. Более наглядное представление о направленности ЭП можно получить, если в пространстве наметить ряд линий так, чтобы векторы напряженности в той или иной точке поля были бы касательными к этим линиям (рис. 9.1).
Такие линии называют линиями вектора напряженности ЭП, или электрическими линиями. Электрические линии всегда направлены от положительно заряженных тел к отрицательно заряженным телам.
Совокупность электрических линий принято называть картиной ЭП (рис. 9.1). Если ЭП создается п зарядами (0„ / е ), то его напряженность равна геометрической сумме напряженностей от каждого из п зарядов в отдельности: т.е. при расчете ЭП применим
метод наложения.
Представим себе ЭП (рис. 9.2), в котором по некоторому пути от точки А до точки В под действием поля движется пробный точечный положительный заряд Q. Со стороны поля к заряду будет приложена сила/ Она направлена по касательной к линии движения и равна (9.2).
Работа на пути от точки А до точки В определится линейным интегралом
где dl — элемент длины пути интегрирования; заряд Q вынесен за знак интеграла, так как в процессе движения величина заряда не меняется.
Таким образом, работа по перемещению заряда равна произведению заряда Q на линейный интеграл от напряженности поля вдоль пути движения заряда:
Рис. 9.2. Перемещение точечного заряда в ЭП
Этот интеграл, определяющийся характеристиками поля по выбранному пути, получил название электрического напряжения между точками А и В.
Выражение (9.5) можно записать в векторной форме:
Напряжение UAB характеризует собой энергетические возможности поля в данной области пространства. Электрическое напряжение является скалярной величиной и в общем случае может приобретать как положительные, так и отрицательные значения.
Единицей электрического напряжения является вольт (В). Если напряжение между двумя точками поля 1 В, то при перемещении заряда в 1 Кл из одной точки в другую будет совершена работа в 1 Дж.
Нетрудно показать, что электрическое напряжение между точками не зависит от пути его вычисления и определяется только положением начальной и конечной точек.
Для пояснения выберем две произвольные точки А и В в поле и рассмотрим два различных пути тип между ними. Очевидно, что оба эти пути составляют замкнутый контур АтВпА (рис. 9.3), для которого справедливо условие — линейный интеграл вектора напряженности в электростатическом поле по любому замкнутому контуру равен нулю:
Линейный же интеграл вектора напряженности по замкнутому контуру можно разбить на два интеграла по двум его участкам
Рис. 9.3. Пути перемещения заряда в ЭП
Изменяя направление интегрирования во втором слагаемом на обратное, т.е. вычисляя линейный интеграл по пути п от А к В, получим
так как перестановка пределов интегрирования приводит к изменению знака интеграла. Отсюда
т.е. оба интеграла и представляемые ими напряжения Uab между точками А и В, вычисленные по разным путям, равны друг другу. Это и является доказательством ранее высказанного тезиса.
Электрический ток, напряжение поймет даже ребенок
Всем привет, на связи с вами снова Владимир Васильев. Новогодние празднования подходят к концу, а значить надо готовиться к рабочим будням, с чем вас дорогие друзья и поздравляю! Хех, только не надо расстраиваться и впадать в депрессию, нужно мыслить позитивно.
Так вот в эти новогодние праздники я как-то размышлял о аудитории моего блога: «Кто он? Кто тот посетитель моего блога, что каждый день заходит почитать мои посты?». Может быть это прошаренный спец зашел из любопытства почитать что я тут накалякал? А может это какой -нибудь доктор радиотехнических наук зашел посмотреть как спаять схему мультивибратора?