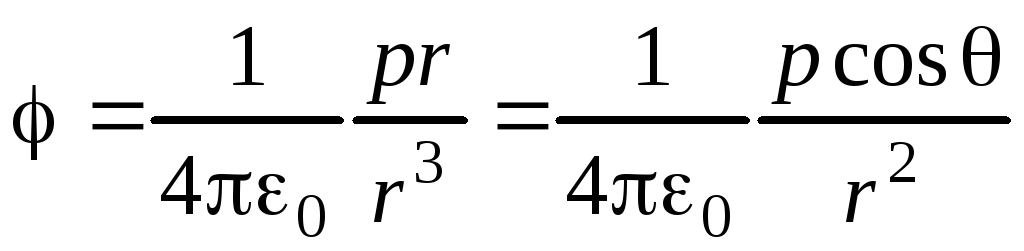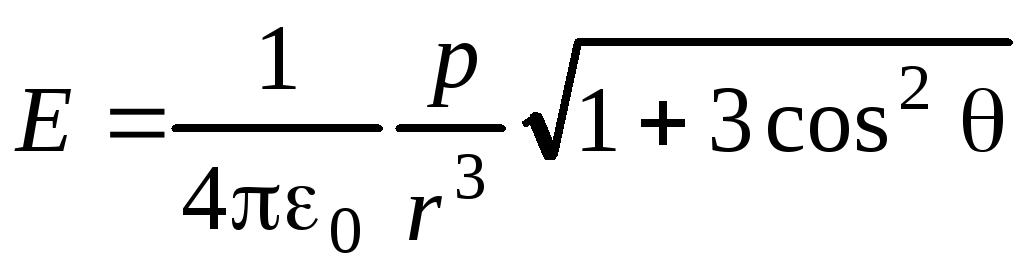Что такое потенциал и что значит его реализовать
Содержание:
Напряженность электрического поля
Напряженность ЭП — характеристика векторная, определяемая в каждой точке и величиной, и направлением. Если в ЭП поместить малый положительный заряд, который своим присутствием не вызовет заметного перераспределения зарядов на телах, создающих поле, то отношение силы, действующей на заряд, к величине заряда Q определяет напряженность поля в данной точке:
Таким образом, Е — силовая характеристика ЭП, определяемая при условии, что внесенный в данную точку поля заряд не исказил поля, существовавшего до его внесения. Отсюда следует, что сила /, действующая на точечный заряд Q , внесенный в поле, будет равна
где Е — напряженность ЭП в точке расположения заряда, а напряженность численно равна силе, действующей на единичный заряд.
Если использовать закон Кулона, который является исторически первым законом из области электромагнитных явлений и определяет силу / взаимодействия двух точечных электрических зарядов Qt и Q,, то сила, действующая по прямой х, соединяющей эти заряды, будет равна
где 8 — абсолютная диэлектрическая проницаемость среды, то модуль напряженности Е в поле точечного заряда можно определить в виде
Поскольку сила, действующая на электрический заряд со стороны ЭП, имеет вполне определенное направление, приходится говорить о направленности свойств этого поля. При этом за направление ЭП в данной точке пространства принимают направление вектора напряженности поля. Более наглядное представление о направленности ЭП можно получить, если, следуя предложению Фарадея, в пространстве наметить ряд линий так, чтобы векторы напряженности в той или иной точке поля были бы касательными к этим линиям (рис. 7.1). Такие линии называют линиями вектора напряженности ЭП, или, короче, электрическими линиями. Электрические линии всегда направлены от положительно заряженных тел к отрицательно заряженным телам.
Совокупность электрических линий принято называть картиной ЭП (рис.
7.1). Если ЭП создается п зарядами (Qni е ), то его напряженность равна геометрической сумме напряженностей от каждого из п зарядов в отдельности:
т.е. при расчете ЭП применим метод наложения.
Представим себе ЭП (рис. 7.2), в котором по некоторому пути от точки А до точки В под действием поля движется пробный точечный положительный заряд Q . Со стороны поля к заряду будет приложена сила /. Она направлена по касательной к линии движения определяется формулой (7.2). Работа А* на пути от точки А до точки В определится линейным интегралом
где dl — элемент длины пути интегрирования; заряд Q вынесен за знак интеграла, так как в процессе движения величина заряда не меняется.
Рис. 7.1. Картина ЭП
Таким образом, работа по перемещению заряда равна произведению заряда Q на линейный интеграл от напряженности ЭП вдоль пути движения заряда. Этот интеграл, определяющийся характеристиками ЭП по выбранному пути, получил название электрического напряжения между точками А и В, который обозначается как указано ниже:
Рис. 7.2. Перемещение точечного заряда в ЭП
Выражение (7.5) можно записать в векторной форме:
Напряжение U iB характеризует собой энергетические возможности ЭП в данной области пространства. Электрическое напряжение является скалярной величиной и в общем случае может приобретать как положительные, так и отрицательные значения.
Единицей электрического напряжения является вольт (В). Если напряжение между двумя точками поля 1 В, то при перемещении заряда в 1 Кл из одной точки в другую будет совершена работа в 1 Дж. Нетрудно показать, что электрическое напряжение между точками не зависит от пути его вычисления и определяется только положением начальной и конечной точек.
Для пояснения выберем две произвольные точки А и В в ЭП и рассмотрим два различных пути т и и между ними (рис. 7.3). Очевидно, что оба эти пути составляют замкнутый контур АтВпА, для которого справедливо условие — линейный интеграл вектора напряженности в ЭП по любому замкнутому контуру равен нулю:
Линейный же интеграл вектора напряженности по замкнутому контуру можно разбить на два интеграла по двум его участкам
Изменяя направление интегрирования во втором слагаемом на обратное, т.е. вычисляя линейный интеграл по пути и от Л к В, получим
так как перестановка пределов интегрирования приводит к изменению знака интеграла. Отсюда
Рис. 7.3. Пути перемещения заряда в ЭП
т.е. оба интеграла и представляемые ими напряжения UiB между точками А и В, вычисленные по разным путям, равны друг другу. Это и является доказательством ранее высказанного тезиса.
Химическая работа
Для однородных многокомпонентных систем открытых систем
- dE=TdS−PdV+∑jμjdmj,{\displaystyle dE=TdS-PdV+\sum _{j}\mu _{j}dm_{j},}
где mj{\displaystyle m_{j}} — масса j{\displaystyle j}-го компонента, μj{\displaystyle \mu _{j}} — химический потенциал этого компонента, по определению равный
| μk≡(∂E∂mk)S,V,{mj≠k}.{\displaystyle \mu _{k}\equiv \left({\frac {\partial E}{\partial m_{k}}}\right)_{S,V,\{m_{j\neq k}\}}.} | (Дефиниция химического потенциала компонента) |
Величину изменение энергии системы за счёт вариации масс составляющих систему веществ
| z≡∑jμjdmj,{\displaystyle z\equiv \sum _{j}\mu _{j}dm_{j},} | (Химическая работа бесконечно малого процесса в открытой однородной системе) |
не имеющую общепринятого названия, чаще всего называют элементарной химической работой, а также массовой работой, работой переноса массы, работой перераспределения масс веществ, энергией, передаваемой при обмене веществом, энергией, передаваемой при переносе массы. Химическая работа не является независимо измеряемой величиной — таковой является сумма энтропийной и химической составляющих изменения энергии в рассматриваемом процессе. Но если положить теплоту бесконечно малого процесса равной
| q≡TdS{\displaystyle q\equiv T\mathrm {d} S} | (Теплота бесконечно малого процесса в открытой однородной системе) |
и учесть, что элементарная работа расширения/сжатия равна
| w=−PdV,{\displaystyle w=-P\mathrm {d} V,} | (Элементарная работа расширения/сжатия в однородной системе) |
то химическая работа может быть вычислена:
- z=∑jμjdmj=dE−q−w=dE−TdS+PdV.{\displaystyle z=\sum _{j}\mu _{j}\mathrm {d} m_{j}=\mathrm {d} E-q-w=\mathrm {d} E-T\mathrm {d} S+P\mathrm {d} V.}
Электрохимический потенциал
Для системы в пространственно неоднородном внешнем поле следует учитывать зависимость химического потенциала компонента от напряжённости поля.
Если система находится в электрическом поле, то химический потенциал электрически заряженных частиц называют электрохимическим потенциалом (термин предложен в 1929 г. Э. А. Гуггенгеймом). Специальный термин понадобился по причине принятого в литературе условного разбиения электрохимического потенциала на неэлектрическую и электрическую части. С теоретической точки зрения такое разделение носит чисто формальный характер, поскольку носителями заряда служат те же самые формульные единицы, с которыми соотносится обычный химический потенциал, и поэтому нет способа раздельного определения его химической и электрической составляющих. Практически же разделение электрохимического потенциала на две части оказывается хорошим приближением в случае заряженных частиц малой массы (электронов и позитронов), для которых вследствие малости их массы вклад неэлектрической части в электрохимический потенциал пренебрежимо мал по сравнению со вкладом электрической составляющей.
Если система находится в гравитационном поле, то условием её равновесия служит постоянство суммы химического потенциала компонента в отсутствие поля и его гравитационного потенциала (конкретизация этого условия для идеального газа даёт барометрическую формулу), и по аналогии с электрохимическим потенциалом химический потенциал компонента в поле тяготения можно назвать гравихимическим потенциалом; химический потенциал компонента в гравитационном поле при наличии электрического поля есть потенциал электрогравихимический. Деление химического потенциала в силовых полях на чисто химическую и полевые (электрическую, магнитную и гравитационную) части носит формальный характер, поскольку нет способа экспериментального определения химической составляющей отдельно от полевых.
Химический потенциал анизотропного тела есть тензор второго ранга, зависящий от тензора напряжений. Как и тензор напряжений, который в изотропных средах становится шаровым, в изотропных средах для задания шарового тензора химического потенциала достаточно единственной скалярной величины.
Формирование людских талантов
Разобравшись в структуре и основных составляющих развития человеческого потенциала, можно рассмотреть его влияние на некоторые сферы жизни общества.
Сама природа изначально заложила в нас достаточный физический и интеллектуальный потенциал. Это свойство дает нам возможность становиться первооткрывателями в тех или иных сферах жизни, выходить живым при неравных схватках с дикой природой, используя навыки первобытного охотника, рыбака, собирателя, и так далее.
Рекомендуем: Психология личности
Человеческая история – это череда непрекращающихся войн, большая часть из которых представляла собой прямое рукопашное сражение, когда от проявления каждым человеком своего физического и духовного потенциала зависело, останется ли он в живых. Потенциально воин постоянно подвергался опасностям со стороны врагов.
Современное же общество практически не нуждается в этом навыке и редко его использует, при этом никто не отменял человеческую потребность выплескивать агрессивный потенциал, что эффективнее всего происходит одновременно с огромными физическими нагрузками на организм. Помимо этого, во многих культурах присутствует социальная необходимость в такого рода деятельности. Это происходит там, где главенствующими ценностями являются смелость, бесстрашие, мужество и тому подобные. Но увы, в обычной жизни такие качества проявить довольно трудно.
Человечество нашло выход из этой ситуации, и это – спорт. По сути, это способ проявить скрытый потенциал в экстремальной ситуации, созданной искусственно. Некоторые виды спорта очень отдаленно напоминают естественные условия, а другие – например, скалолазание, горные походы, спортивный туризм, охота и рыбалка – максимально приближаются к реальным задачам наших предков в обычной жизни. Отсюда и возникает необходимость в полноценных острых ощущениях.
Рекомендуем: Задатки и способности человека
Наше общество, индустриальное и постиндустриальное, полно людей, которые готовы тратить деньги, время и силы для того, чтобы как можно сильнее оторваться от привычной современной жизни, приблизиться к границам своих возможностей – физических, психических и эмоциональных. Испытать себя по полной, лишь так ощутив себя полноценным и по-настоящему живым. Потенциал личности настолько силен внутри нас, что постоянно стремится вырваться наружу.
Повсеместно проводятся специальные курсы и тренинги по выживанию в экстремальных условиях, в диких удаленных местах и т.д. Человек готов отдать много сил, чтобы попробовать себя в борьбе один на один с дикой природой. Это стремление живет внутри нас, оно сформировано тысячелетиями эволюции.
Однако в современном мире у человека практически нет мест, где он может раскрывать этот свой потенциал. Казалось бы, эти навыки были жизненно необходимы, и буквально за последние двести лет, прошедшие с момента начала индустриализации мира, возможность реализовать свой потенциальный запал напрочь исчезла. Отсюда и все эти экстремальные увлечения.
Однако стоит обратить внимание на то, что человек, который для своего пропитания, выживания и в наше время постоянно отстаивает у дикой природы право на жизнь, вряд ли согласится пойти в горы с туристической группой просто так или сплавиться на байдарке по горной реке. Потенциальный риск доступен ему и в повседневной жизни
Физика для средней школы
Потенциал
Из механики известно, что работа консервативных сил связана с изменением потенциальной энергии. Система «заряд — электростатическое поле» обладает потенциальной энергией (энергией электростатического взаимодействия). Поэтому, если не учитывать взаимодействие заряда с гравитационным полем и окружающей средой, то работа, совершаемая при перемещении заряда в электростатическом поле, равна изменению потенциальной энергии заряда, взятому с противоположным знаком:
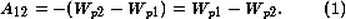
Если Wp2 = 0, то в каждой точке электростатического поля потенциальная энергия заряда q равна работе, которая была бы совершена при перемещении заряда q из данной точки в точку с нулевой энергией.
Пусть электростатическое поле создано в некоторой области пространства положительным зарядом q (рис. 1).
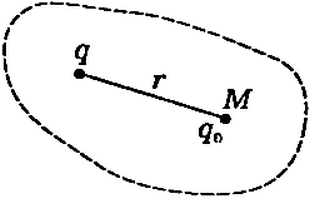
Рис. 1
Будем помещать в точку М этого поля различные пробные положительные заряды q. Потенциальная энергия их различна, но отношение для данной точки поля и служит характеристикой поля, называемой потенциалом поля в данной точке:
Единицей потенциала в СИ является вольт (В) или джоуль на кулон (Дж/Кл).
Потенциалом электростатического поля в данной точке называют скалярную физическую величину, характеризующую энергетическое состояние поля в данной точке пространства и численно равную отношению потенциальной энергии, которой обладает пробный положительный заряд, помещенный в эту точку, к значению заряда.
Потенциал — это энергетическая характеристика поля в отличие от напряженности поля, являющейся силовой характеристикой поля.
Необходимо отметить, что потенциальная энергия заряда в данной точке поля, а значит, и потенциал зависят от выбора нулевой точки. Нулевой эта точка называется потому, что потенциальную энергию (соответственно потенциал) заряда, помещенного в эту точку поля, уславливаются считать равной нулю.
Нулевой уровень потенциальной энергии выбирается произвольно, поэтому потенциал можно определить только с точностью до некоторой постоянной, значение которой зависит от того, в какой точке пространства выбрано его нулевое значение.
В технике принято считать нулевой точкой любую заземленную точку, т.е. соединенную проводником с землей. В физике за начало отсчета потенциальной энергии (и потенциала) принимается любая точка, бесконечно удаленная от зарядов, создающих поле. Если нулевая точка выбрана, то потенциальная энергия (соответственно и потенциал в данной точке) заряда q становится определенной величиной.
На расстоянии r от точечного заряда q, создающего поле, потенциал определяется формулой
При указанном выше выборе нулевой точки потенциал в любой точке поля, создаваемого положительным зарядом q, положителен, а поля, создаваемого отрицательным зарядом, отрицателен:
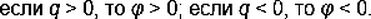
По этой формуле можно рассчитывать потенциал поля, образованного равномерно заряженной проводящей сферой радиусом R в точках, находящихся на поверхности сферы и вне ее. Внутри сферы потенциал такой же, как и на поверхности, т.е.
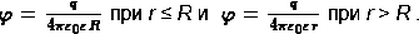
Если электростатическое поле создается системой зарядов, то имеет место принцип суперпозиции: потенциал в любой точке такого поля равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом в отдельности:
Зная потенциал поля в данной точке, можно рассчитать потенциальную энергию заряда q0 помещенного в эту точку: Wp1 = q. Если положить, что Wp2 = 0, то из уравнения (1) будем иметь
Потенциальная энергия заряда q в данной точке поля будет равна работе сил электростатического поля по перемещению заряда q0 из данной точки в нулевую. Из последней формулы имеем
Потенциал поля в данной точке численно равен работе по перемещению единичного положительного заряда из данной точки в нулевую (в бесконечность).
Потенциальная энергия заряда q помещенного в электростатическое поле точечного заряда q на расстоянии r от него,
Если q и q — одноименные заряды, то , если q и q — разные по знаку заряды, то .
Отметим еще раз, что по этой формуле можно рассчитать потенциальную энергию взаимодействия двух точечных зарядов, если за нулевое значение Wp выбрано ее значение при r = бесконечности.
Если электростатическое поле образовано системой n точечных электрических зарядов, то потенциальная энергия системы определяется по формуле
где — потенциал поля, созданного всеми зарядами, кроме заряда qi, в той точке поля, где находится заряд qi.
Электрохимические устройства и процессы
Так как окислительно-восстановительные реакции сопровождаются переносом заряда, то их можно осуществлять действием электрического тока, и наоборот, — получать электрический ток за счет их протекания. В соответствующих процессах и устройствах используются электроды и электродные потенциалы.
Понятие об электродном потенциале.
Если металлическую пластинку опустить в воду или раствор, содержащий ионы этого металла, то на границе раздела металл-раствор за счет процессов растворения-осаждения металла возникает разность или скачок потенциала, который зависит от природы металла, концентрации раствора, а также от температуры. Этот скачок называется электродным потенциалом данного металла. Указанное равновесие выражается уравнением, учитывающим гидратацию иона:
Ме + mH2O Me n+(H2O)m + ne .
в растворе на металле
Потенциал, соответствующий данному равновесию, называется равновесным электродным потенциалом.
Значение j нельзя определить по абсолютной величине. Поэтому потенциалы всех электродов определяют по отношению к стандартному водородному полуэлементу (электроду) (рис. 7.1), потенциал которого принимают равным нулю: jо298 (2Н+ Н2) = 0. Стандартный водородный электрод состоит из сосуда с 1н. раствором кислоты, в которую опущен платиновый электрод, контактирующий с газообразным водородом, находящимся под давлением Р = 101,3 кПа.
Рис. 7.1. Стандартный водородный электрод
На электроде устанавливается равновесие 2Н+р + 2? Н2 (г). Нулевое значение jо для этого электрода определяется и тем, что DGf (Н+) = DGf (Н2) = 0. Платина используется вследствие ее инертности, а также потому, что она является катализатором переноса электрона (процесс установления равновесия ускоряется, но само состояние равновесия, то есть функции DН, DU, DG, DS, остается неизменными при постоянной температуре).
Потенциалы, определенные относительно стандартного электрода в стандартных условиях (то есть jо298) табулированы. Для металлов по химическим данным (Н.Н. Бекетовым), а затем путем измерения jо298 установлен ряд активности металлов, который в настоящее время имеет назавание электрохимический ряд напряжения металлов (табл.12.1).
Таблица 12.1
Стандартные электродные потенциалы j некоторых металлов
(ряд напряжения)
| Электрод | j , В | Электрод | j , В | Электрод | j ,В |
| Li+/Li | -3,045 | Mn2+/Mn | -1,18 | 2H+/H2 | 0,000 |
| Rb+/Rb | -2,925 | Cr2+/Cr | -0,913 | Sb3+/Sb | +0,20 |
| K+/K | -2,924 | Zn2+/Zn | -0,763 | Bi3+/Bi | +0,215 |
| Сs+/Cs | -2,923 | Cr3+/Cr | -0,74 | Cu2+/Cu | +0,34 |
| Ba2+/Ba | -2,90 | Fe2+/Fe | -0,44 | Сu+/Cu | +0,52 |
| Ca2+/Ca | -2,87 | Сd2+/Cd | -0,403 | Hg22+/2Hg | +0,79 |
| Na+/Na | -2,714 | Сo2+/Co | -0,27 | Ag+/Ag | +0,80 |
| Mg2+/Mg | -2,37 | Ni2+/Ni | -0,25 | Hg2+/Hg | +0,85 |
| Al3+/Al | -1,70 | Sn2+/Sn | -0,136 | Pt2+/Pt | +1,19 |
| Ti2+/Ti | -1,603 | Pb2+/Pb | -0,127 | Au3+/Au | +1,50 |
| Zr4+/Zr | -1,58 | Fe3+/Fe | -0,037 | Au+/Au | +1,70 |
Электродный потенциал, измеренный при стандартных условиях (Т = 298К; = 1моль/л) относительно стандартного водородного электрода, называется стандартным электродным потенциалом металла и обозначается j. Стандартный электродный потенциал является количественной характеристикой химической активности металла, т.е. его способности отдавать свои валентные электроны и переходить в раствор в виде ионов.
Основные свойства ряда напряжения.
Чем меньше величина j, тем сильнее выражена восстановительная активность металла.
Если условия отличаются от стандартных, то для расчета электродного потенциала используется формула Нернста:
где j — стандартный электродный потенциал металла,
n — число электронов, принимающих участие в процессе,
F — постоянная Фарадея (96500 Кл/моль),
R — универсальная газовая постоянная (8,31 Дж·моль-1·К-1),
Т – абсолютная температура (К).
Если в приведенном уравнении заменить постоянные числовыми значениями, то оно примет следующий вид:
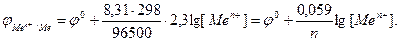
Из формулы Нернста видно, что при стандартной концентрации катионов, равной 1М φ = j , т.е. равновесный электродный потенциал металла равен его стандартному потенциалу.
Компьютерное моделирование
Существуют
различные методы решения дифференциальных
уравнений. В некоторых частных случаях
решение удается получить аналитически
(выразить через элементарные функции),
но чаще всего приходится использовать
численные методы и компьютерные расчеты.
Будем
исходить из того, что уже разработана
компьютерная программа, которая с
высокой точностью находит решение
уравнения Лапласа
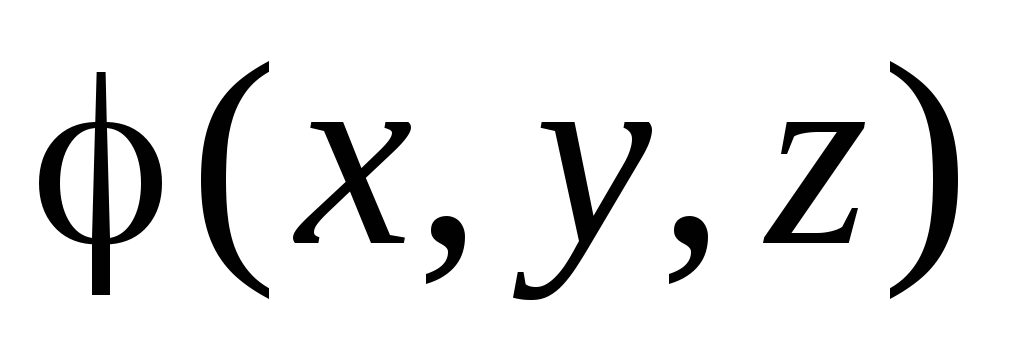 ,
,
удовлетворяющее заданным граничным
условиям на поверхности тел, входящих
в систему. Такое решение будет совпадать
с экспериментом, если все проводники
являются однородными, неподвижными и
в поле отсутствуют диэлектрики. Поэтому
к результатам таких компьютерных
расчетов можно относиться как к
«компьютерному эксперименту»,
моделирующему эксперимент реальный.
Наша задача состоит в выполнении
«компьютерного эксперимента» и в
анализе получаемых результатов.
Работа
с компьютерными программами обычно
включает два этапа. Во-первых, необходимо
убедиться в правильности работы
программы. Для этого программу «испытывают»
на частных задачах и в специальных
случаях, когда решение точно (или
приближенно) известно. Компьютерный
эксперимент должен подтверждать
известные закономерности, а также
показывать отклонение от теоретических
результатов, полученных в рамках
некоторых предположений, нарушающихся
в компьютерном эксперименте.
Например,
потенциал и модуль вектора напряженности
электрического поля, созданного точечнымдиполем в точке, положение которой
задано радиус-вектором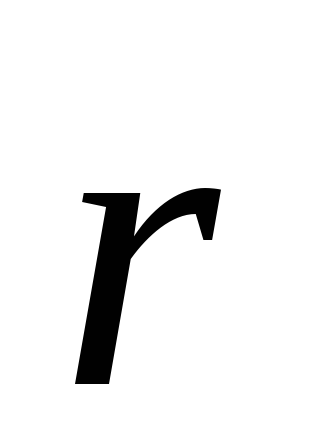 (рис.5),
(рис.5),
определяются формулами
где
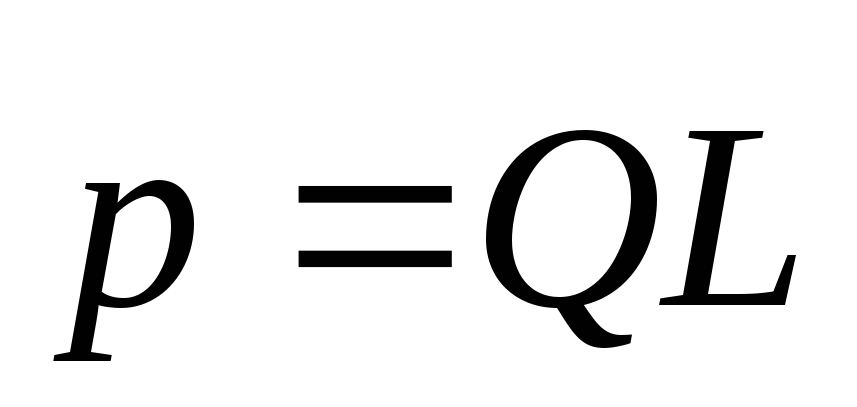 электрический момент диполя (дипольный
электрический момент диполя (дипольный
момент),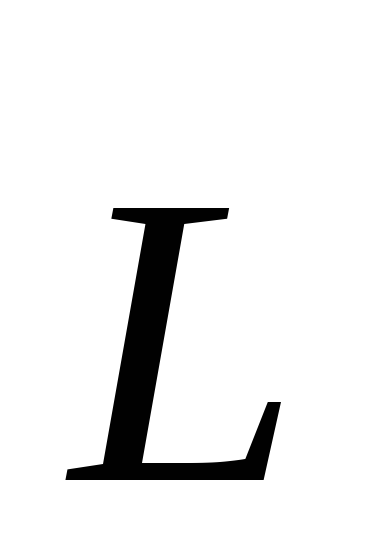 – вектор, проведенный ототрицательногозаряда к положительному,
– вектор, проведенный ототрицательногозаряда к положительному, — угол между векторами
— угол между векторами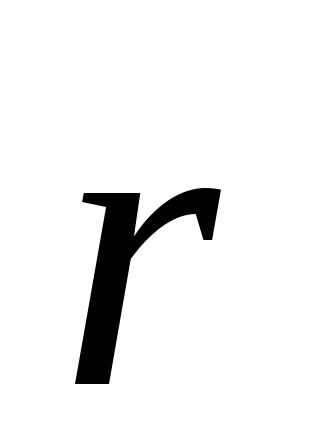 и
и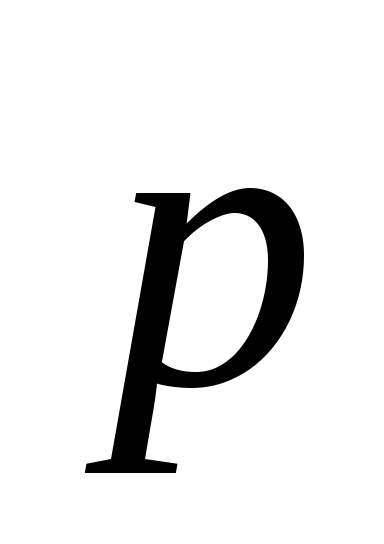 .
.
Формулы (5), (6) получены для точечного
диполя, когда длина
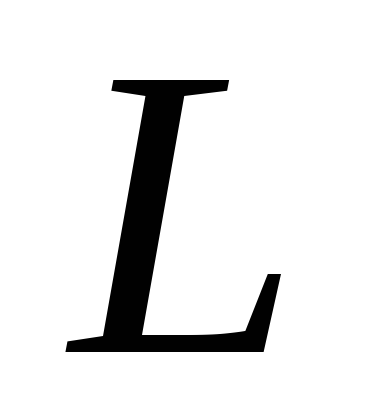 пренебрежимо мала по сравнению с
пренебрежимо мала по сравнению с
расстоянием от диполя до точки наблюдения.
Поэтому при нарушении условия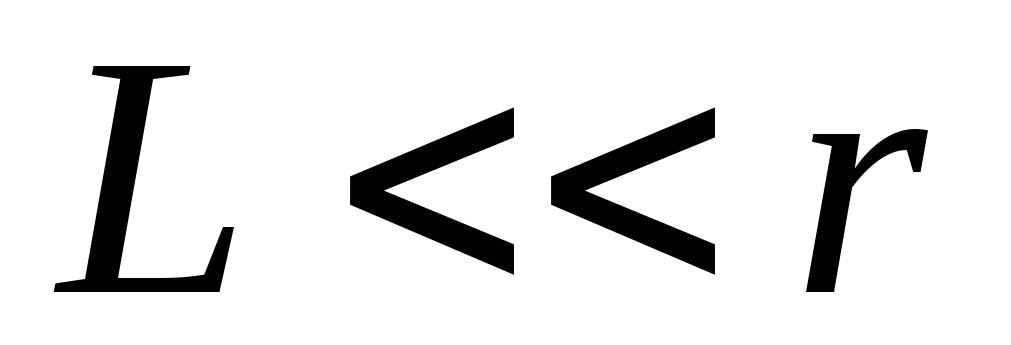 должны наблюдаться отклонения расчетов
должны наблюдаться отклонения расчетов
по формулам (5), (6) от результатов
компьютерного эксперимента. Причем эти
отклонения должны уменьшаться с
увеличением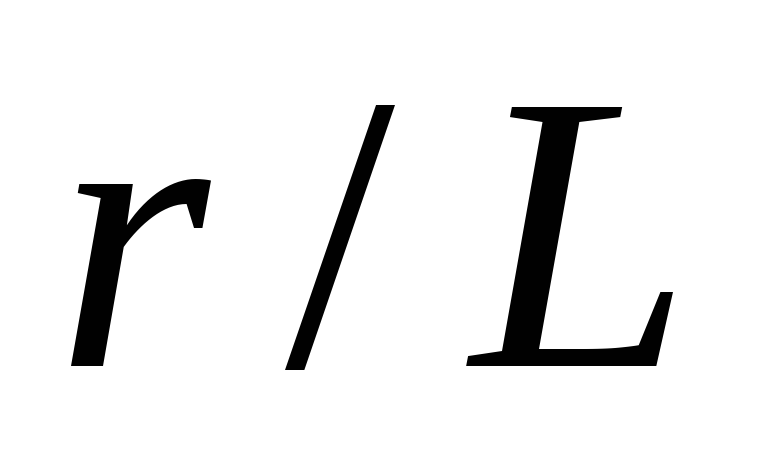 .
.
После
«испытания» компьютерной программы
можно приступить к поиску новых
закономерностей. Вам будет предложено
исследовать распределение заряда по
поверхности заряженного проводящего
эллипсоида, а также по поверхности
проводящей сферы, расположенной в поле
точечного заряда. Эти задачи являются
для Вас новыми в том смысле, что их не
удается решить, напрямую воспользовавшись
формулой (1) и принципом суперпозиции.
Для
«экспериментального» определения
плотности поверхностного заряда следует
воспользоваться результатом, строго
вытекающим из теоремы Гаусса: во внешнем
пространстве вблизи поверхности
проводника поле
 перпендикулярно к поверхности проводника
перпендикулярно к поверхности проводника
и определяется формулой
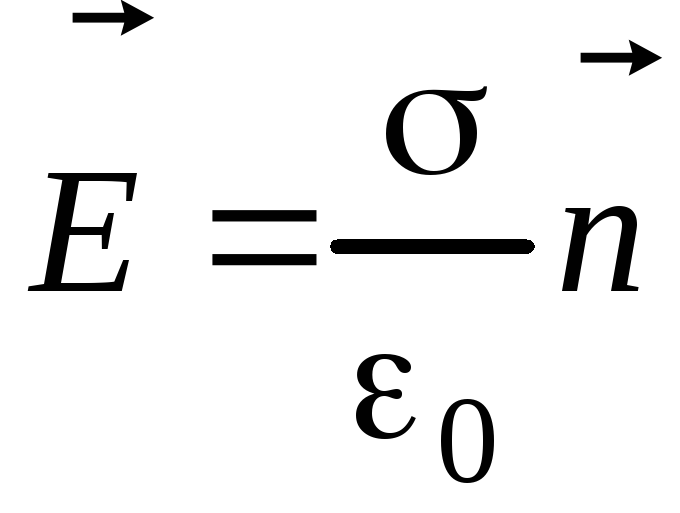 ,
,
(7)
где
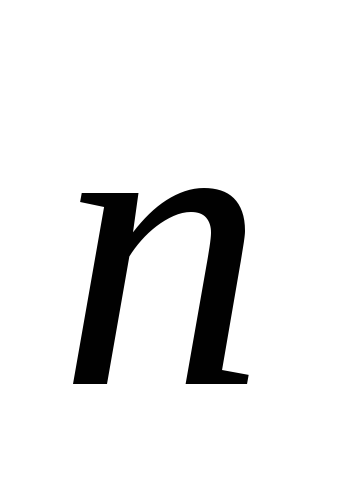 —
—
нормаль, проведенная наружу от поверхности
проводника, — поверхностная плотность заряда в
— поверхностная плотность заряда в
данной точке поверхности.
Литература
- Химический потенциал // : / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- Большая физическая энциклопедия в 5-ти томах. Гл. ред. А. М. Прохоров. Москва «Советская энциклопедия» 1988 г.
- Гуггенгейм. Современная термодинамика, изложенная по методу У. Гиббса / Пер. под ред. проф. С. А. Щукарева. — Л.—М.: Госхимиздат, 1941. — 188 с.
- Заславский Б. В. Краткий курс сопротивления материалов. — М.: Машиностроение, 1986. — 328 с.
- Зимон А. Д. Коллоидная химия: Общий курс. — 6-е изд. — М.: Красанд, 2015. — 342 с. — ISBN 978-5-396-00641-6.
- Мейз Дж. Теория и задачи механики сплошных сред. — М.: Мир, 1974. — 319 с.
- Румер Ю. Б., Рывкин М. Ш. Термодинамика, статистическая физика и кинетика. М., Наука, 1977. 552 с.
- Русанов А. И. Лекции по термодинамике поверхностей. — СПб.—М.—Краснодар: Лань, 2013. — 237 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1487-1.
- Салем Р. Р. Физическая химия. Термодинамика. — М.: Физматлит, 2004. — 351 с. — ISBN 5-9221-0078-5.
- Тамм М. Е., Третьяков Ю. Д. Неорганическая химия. Том 1. Физико-химические основы неорганической химии / Под. ред. акад. Ю. Д. Третьякова. — М.: Академия, 2004. — 240 с. — (Высшее профессиональное образование). — ISBN 5-7695-1446-9.
- Тер Хаар Д., Вергеланд Г. Основы термодинамики / Пер. с англ.. — М.: Вузовская книга, 2006. — 200 с. — ISBN 5-9502-0197-3.
- Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5: Стробоскопические приборы — Яркость. — 760 с. — ISBN 5-85270-101-7.
- Guggenheim E. A. Thermodynamics: An Advanced Treatment for Chemists and Physicists. — Amsterdam: North-Holland, 1985. — xxiv + 390 с. — ISBN 0 444 86951 4.