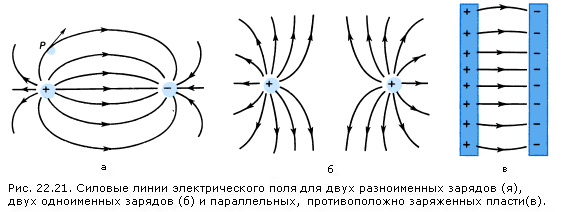
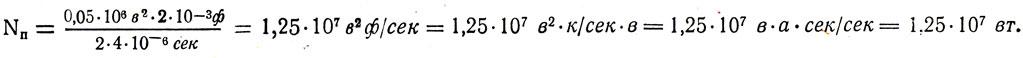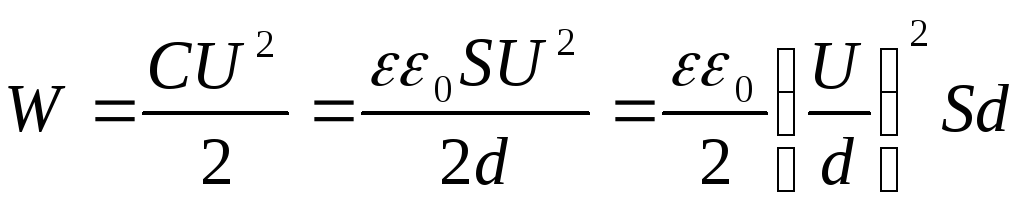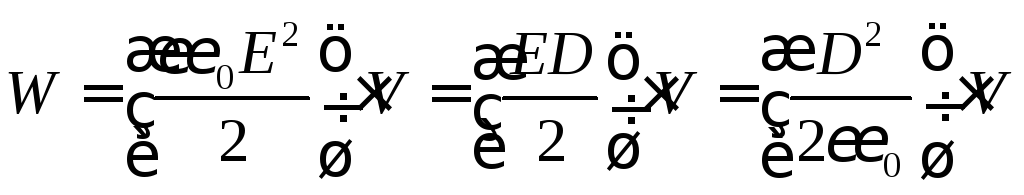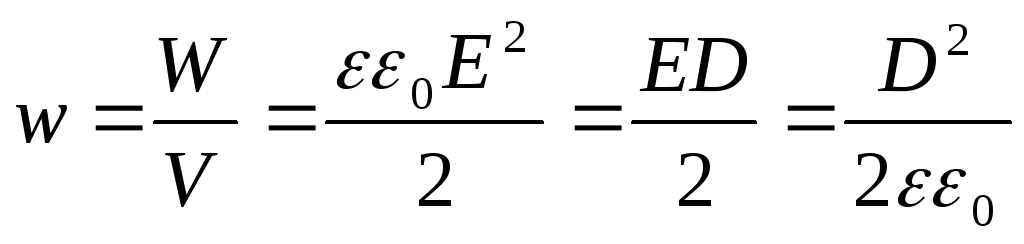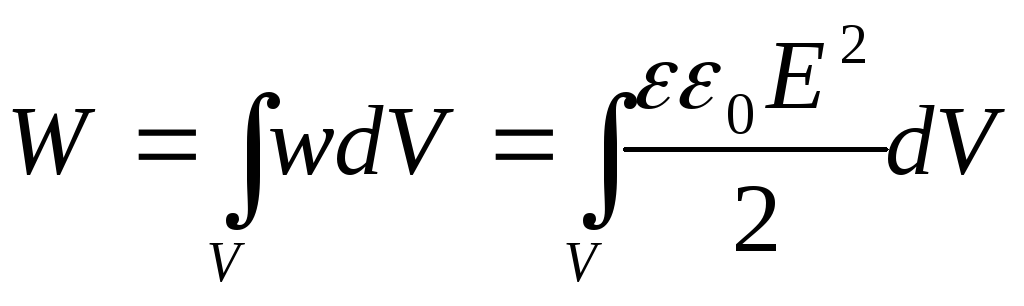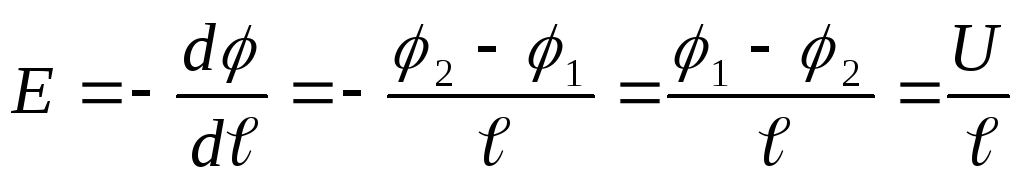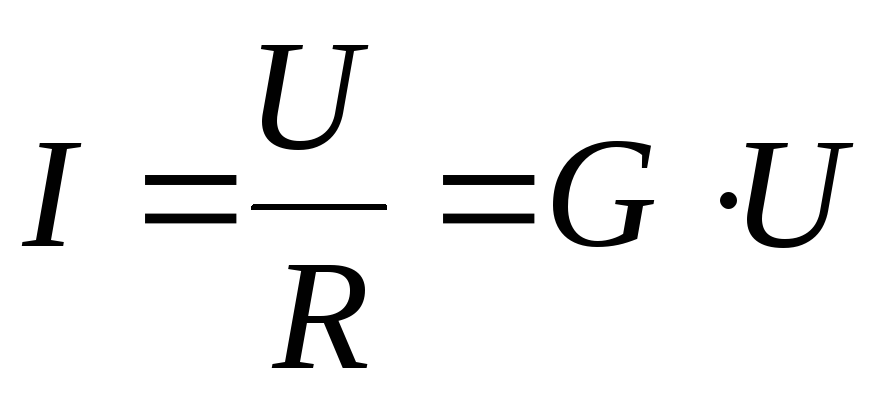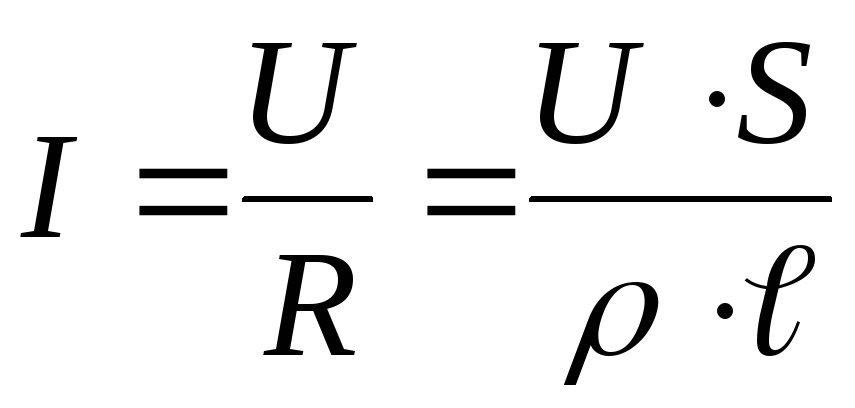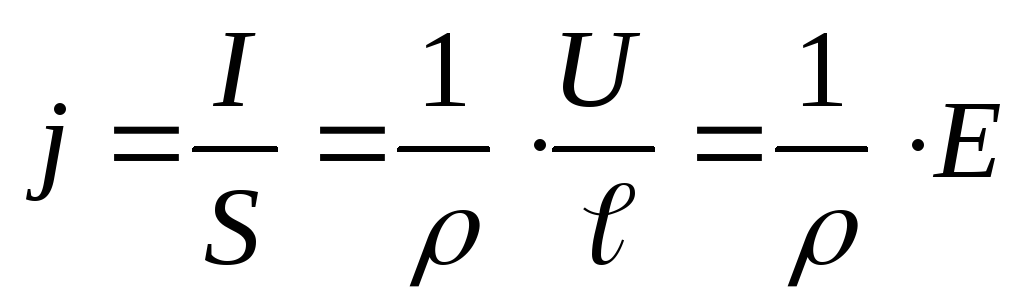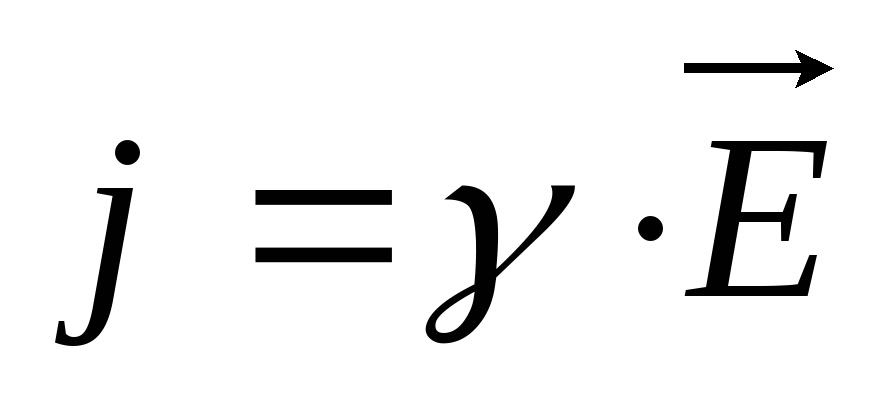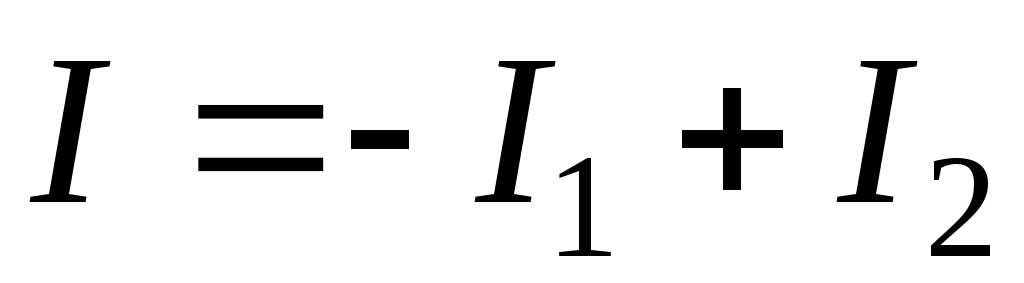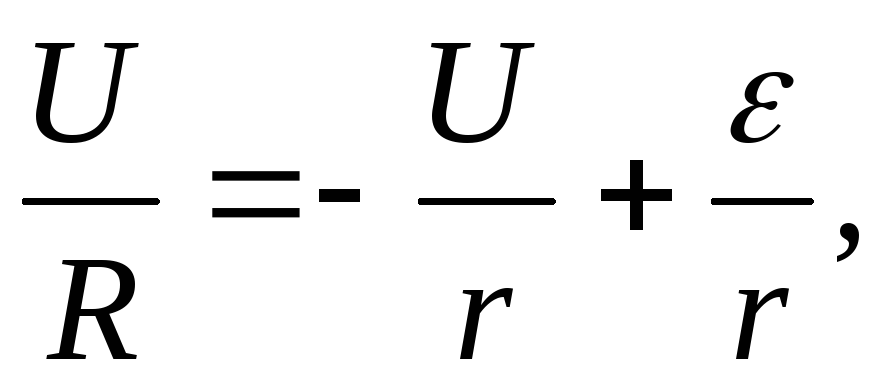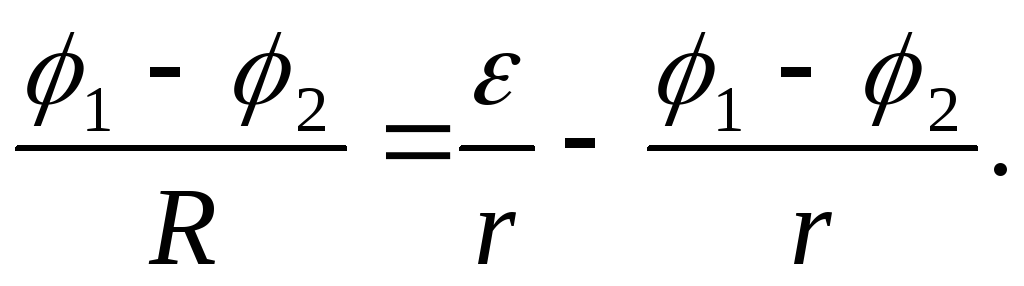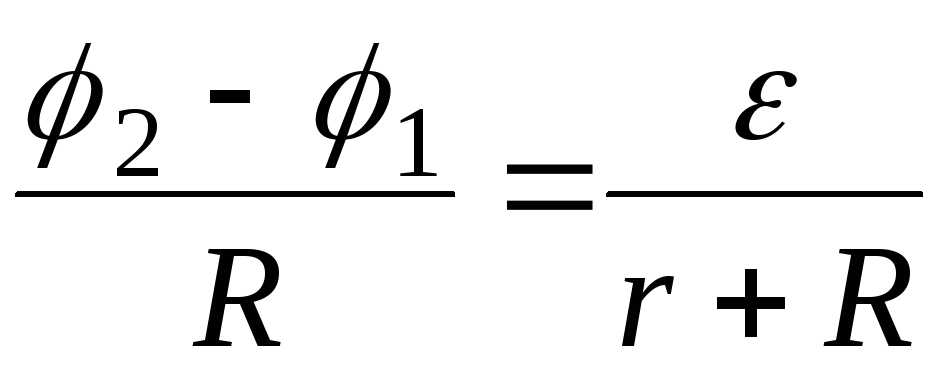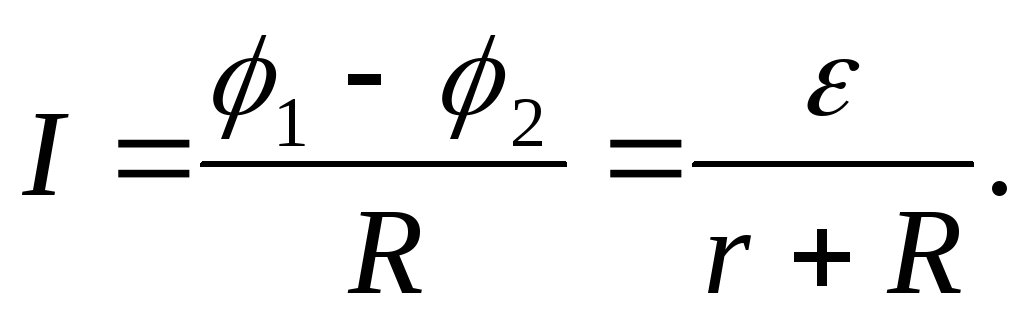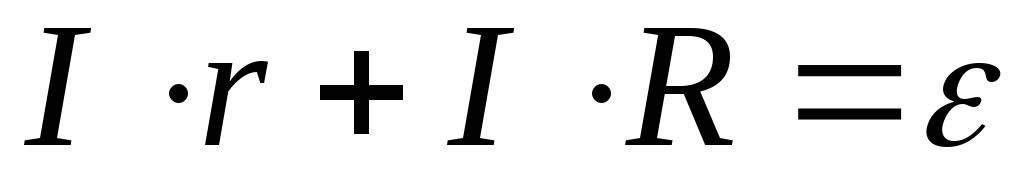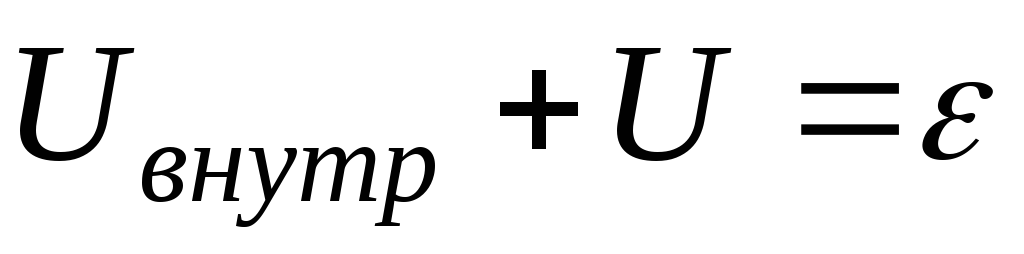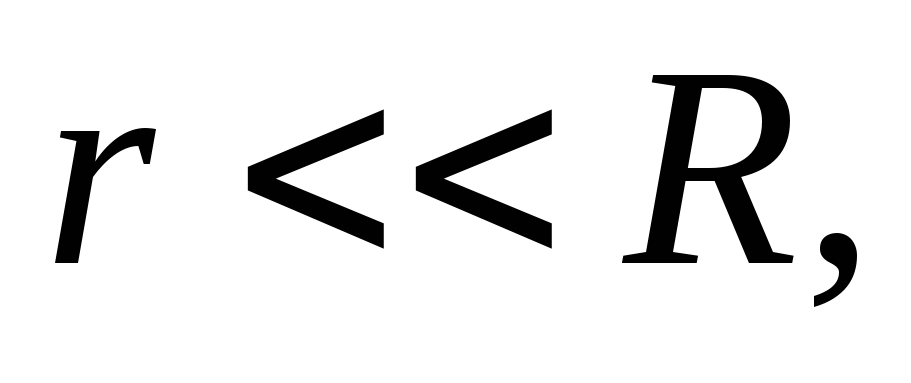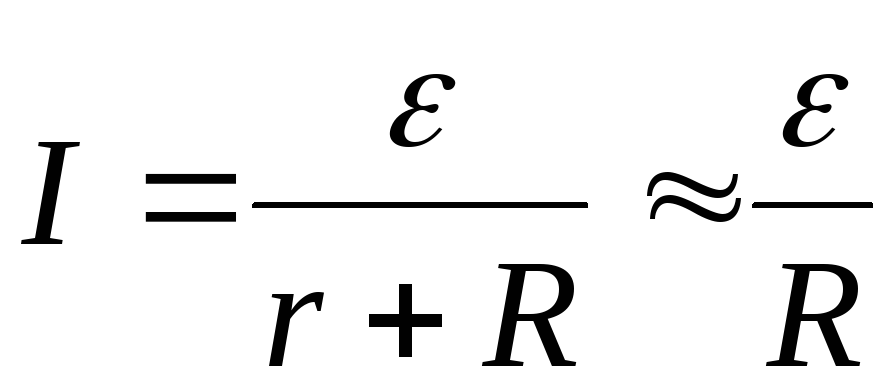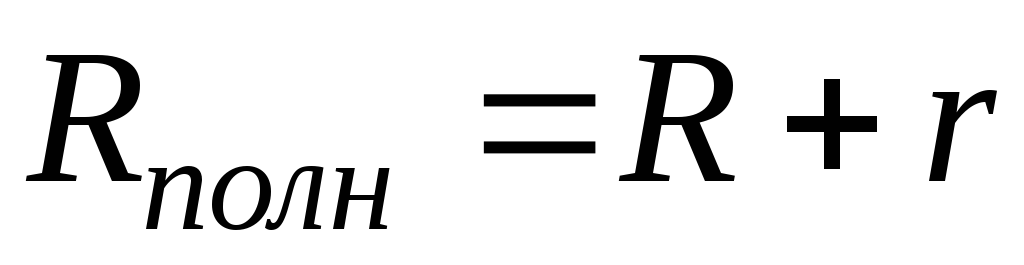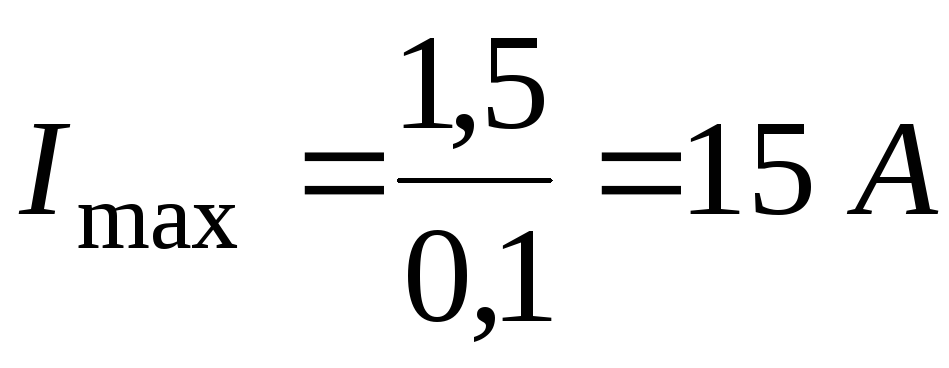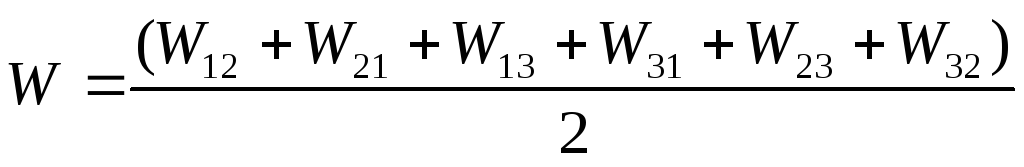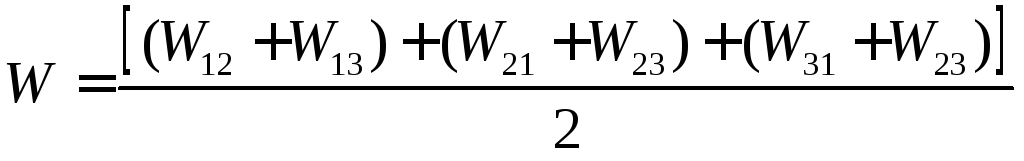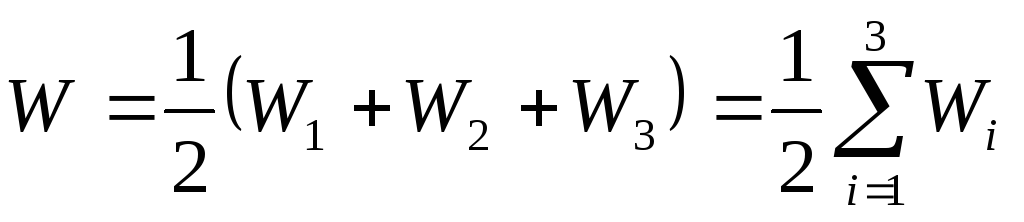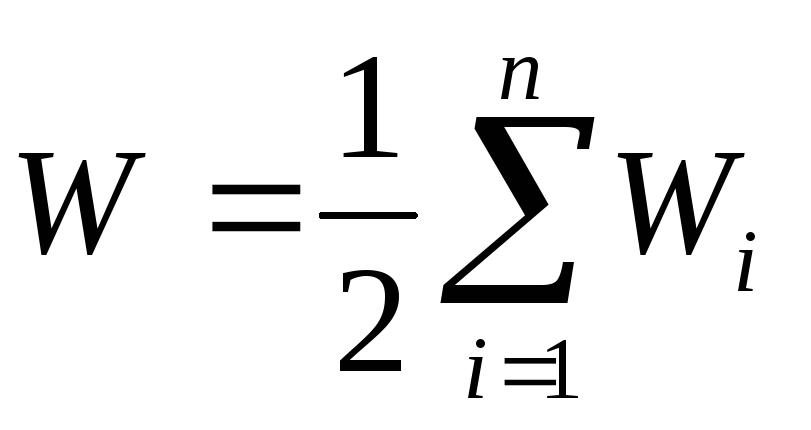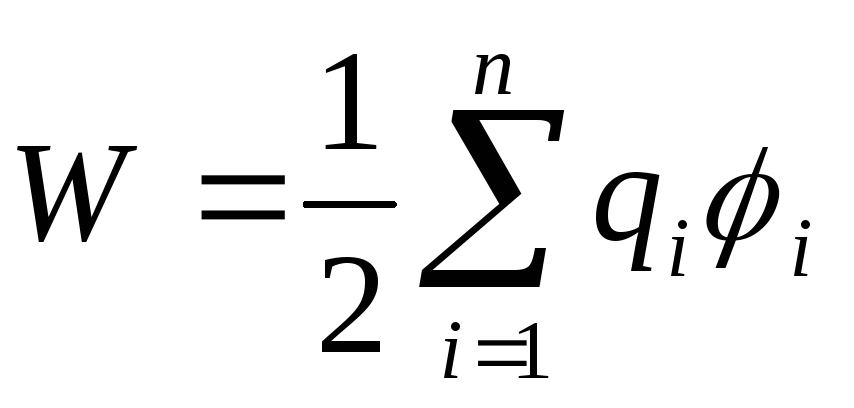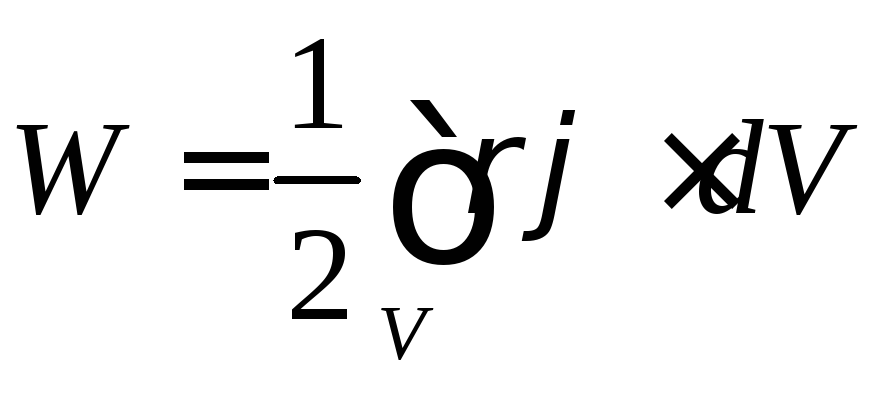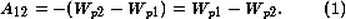Все формулыЭнергия заряженного конденсатораЗапись навигация

53. Энергия электрического поля конденсатора

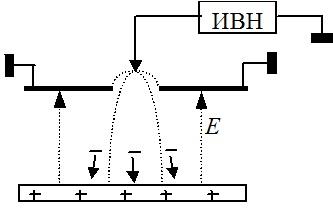
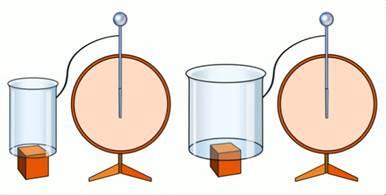
Поставив переключатель в положение 1, зарядим конденсатор (рис.71). Теперь между его обкладками (пластинами) имеется электрическое поле. Поле — вид материи. Она обладает массой и энергией. Значит электрическое поле обладает энергией. Поставив переключатель в положение 2, подключим заряженный конденсатор к лампочке. Она ярко вспыхивает. Энергия электрического поля конденсатора превратилась во внутреннюю энергию нити лампочки и в энергию излучения.

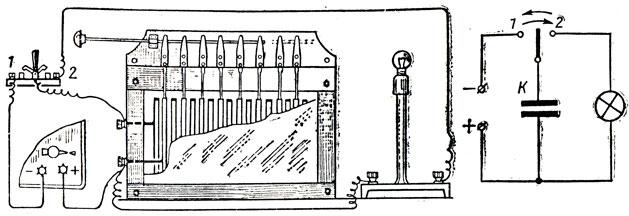Рис. 71. Энергия заряженного конденсатора

При разряде конденсатора за счет энергии Е его электрического поля совершается работа А по перемещению электронов, образующих ток. При разряде конденсатора напряжение (разность потенциалов) между его обкладками меняется от U (которое стало на конденсаторе, после его зарядки) до нуля. Поэтому средняя величина напряжения на конденсаторе

На перемещение электронов с общим зарядом в 1 к электрическое поле затрачивает энергии При перемещении электронов с общим зарядом q кулонов оно затрачивает энергии в q раз больше. Величина работы по перемещению равна энергии, накопленной в конденсаторе, при его зарядке:

A = E = U_срq,

или

где q = CU.

Заменив q, получим формулу энергии электрического поля конденсатора:

Включив половину электроемкости (60 мкф) конденсатора, зарядим его, а затем разрядим на лампочку. Увеличив электроемкость в два раза, зарядим конденсатор (при прежнем напряжении) и снова разрядим его на лампочку. Замечаем, что во втором случае вспышка лампочки была ярче: с увеличением электроемкости конденсатора увеличилась энергия его поля. Не меняя электроемкости конденсатора, зарядим его от напряжения 40 в и разрядим на лампочку, а затем то же самое сделаем при напряжении 80 в. Видим, что чем больше напряжение между пластинами конденсатора, тем больше энергия его электрического поля, о чем свидетельствует различная яркость вспышки лампы.

Энергия электрического поля конденсатора используется, например для получения электрических колебаний в радиоприемниках, радиопередатчиках, телевизорах, для получения кратковременного тока в фотовспышках, радиолокаторах, для получения высоких температур, при исследовании термоядерных реакций.

Задача 22. Импульсная сварка осуществляется с помощью разряда конденсатора электроемкостью 2000 мкф при напряжении на его обкладках 1000 в. Определить полезную мощность импульса, если продолжительность разряда 4 мксек, а к. п. д. установки 5%.

Полезная мощность установки Из формулы полезно израсходованная энергия E_п = ηE. Здесь Е — энергия электрического поля конденсатора, Тогда

Следовательно,

Вычислим:

Отв.: N_п = 12500 квт.

3 Энергия и плотность энергии электрического поля

Выразим энергию заряженного плоского
конденсатора через напряженность
электрического поля. Подставим в формулу

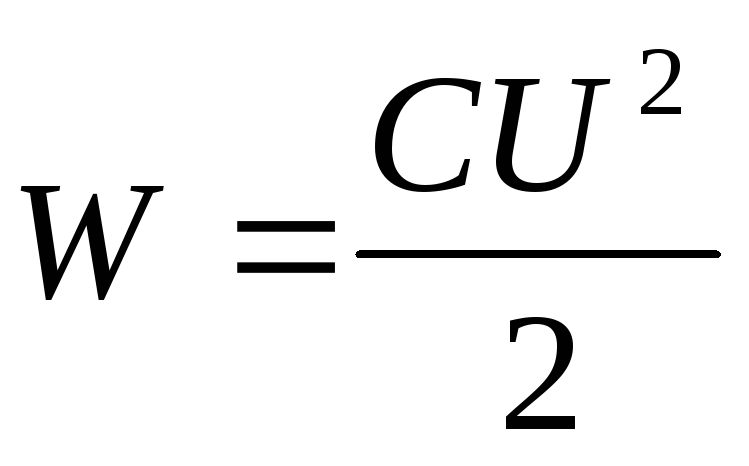выражение,
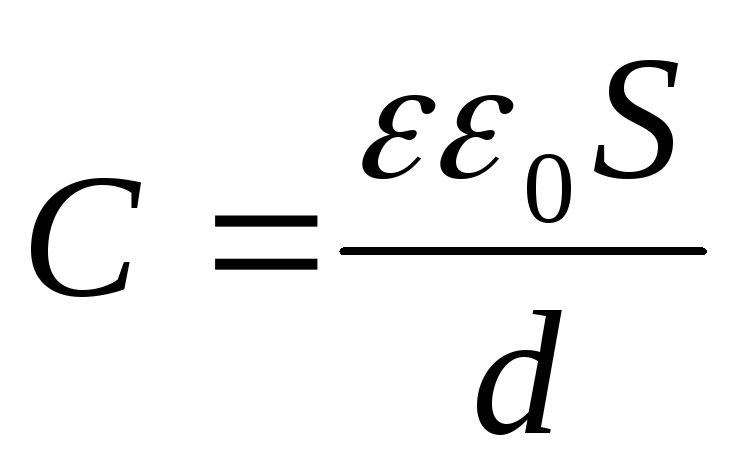получим

.

Поскольку
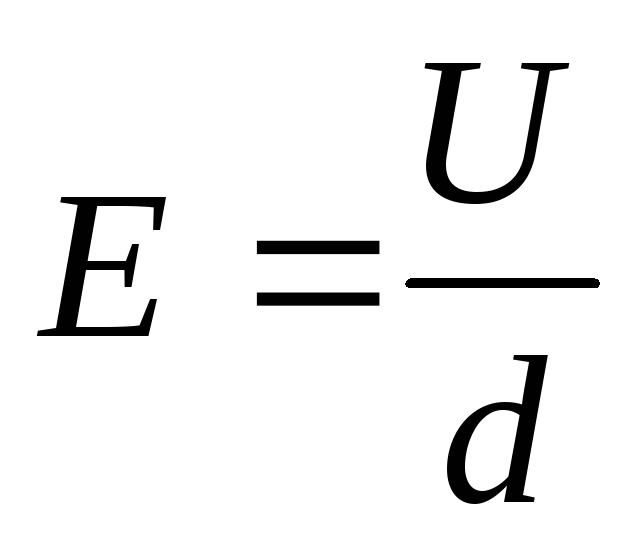и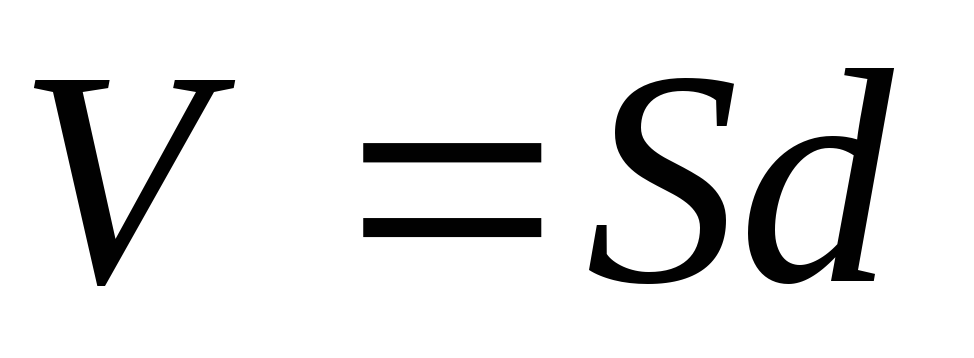(объем между обкладками конденсатора),
то

.

Как будет показано в следующей главе,
вспомогательной характеристикой поля
в веществе является вектор электрического
смещения
,
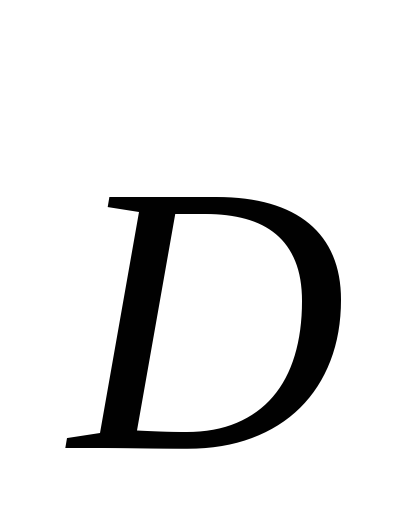который связан с вектором напряженности
электрического полясоотношением.

С учетом этого соотношения полученную
формулу можно представить в виде:

(3.6)

Эти формулы справедливы для однородного
поля, заполняющего объем
.

Энергия распределена по объему
конденсатора равномерно. Следовательно,
в единице объема поля содержится энергия

(3.7)

Выражения (3.7) определяют плотность
энергии электрического поля.

Формулы (3.7) справедливы для любого
электрического поля. Если поле неоднородно,
то плотность энергии в некоторой точке
определяется по формулам (3.7) подстановкой
значений
(или)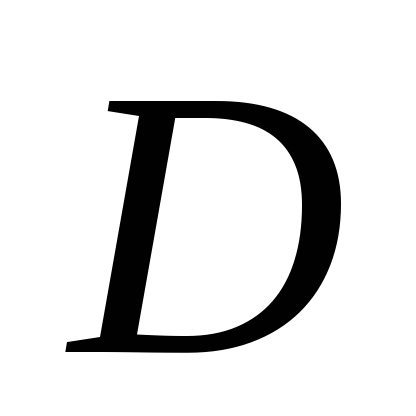
ив этой точке.

Зная плотность энергии в каждой точке,
можно найти энергию поля, заключенную
в любом объеме
.
Для этого нужно вычислить интеграл

(3.8)

2. Закон Ома. Сопротивление и электропроводность проводника

Рассмотрим
цилиндрический проводник длиной
.

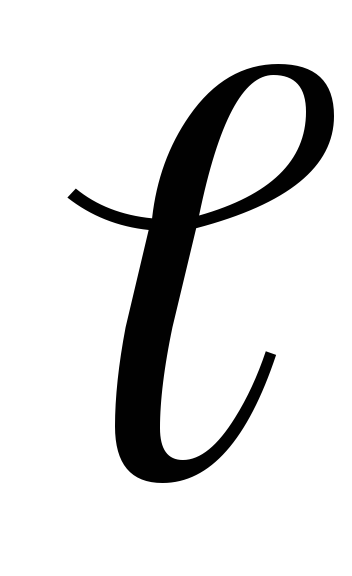Для того, чтобы в
проводнике существовал постоянный ток
,
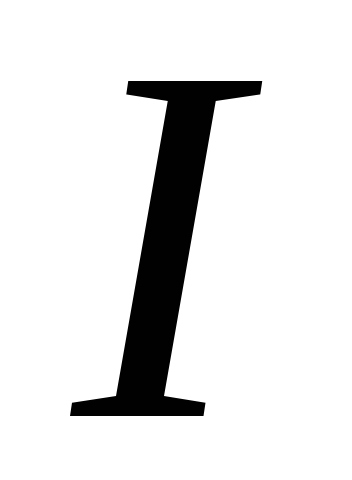необходимо внутри проводника создать
постоянное электрическое поле с
напряженностью.
Напряженность электрического поля в
проводнике существует тогда, когда в
нем имеется градиент потенциала:

(2.2)

Где
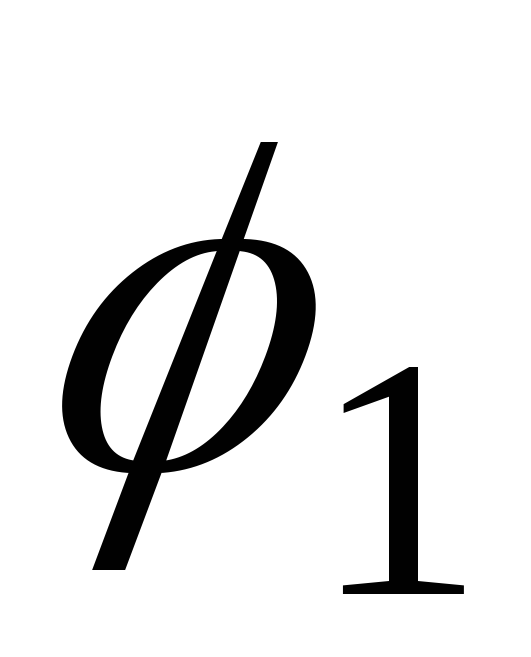и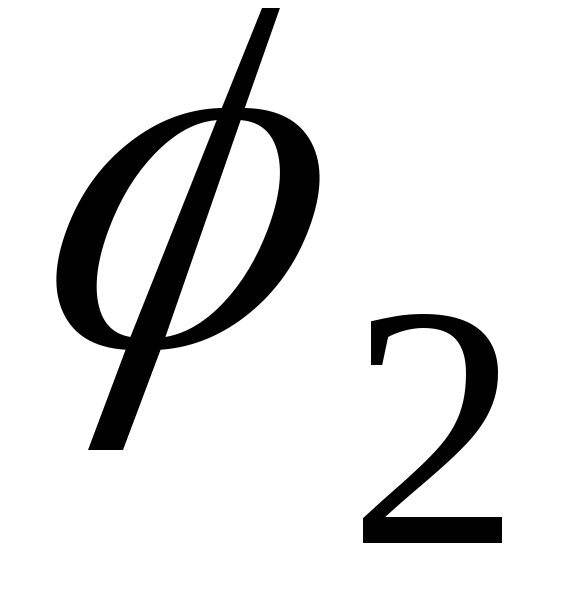— электрические потенциалы на концах
проводникаU
— напряжение, приложенное к проводнику.
При изменении напряжения U
изменяется ток в проводнике по закону
Ома

(2.3)

где R
– электрическое сопротивление
проводника;
– проводимость
проводника.

В системе СИ
сопротивление измеряется в Ом. 1 Ом –
сопротивление такого проводника, в
котором при напряжении 1В идет ток в 1
А. Сопротивление R
зависит от материала, из которого сделан
проводник, его геометрических размеров
и формы. Для цилиндрических проводников
справедливо соотношение

,
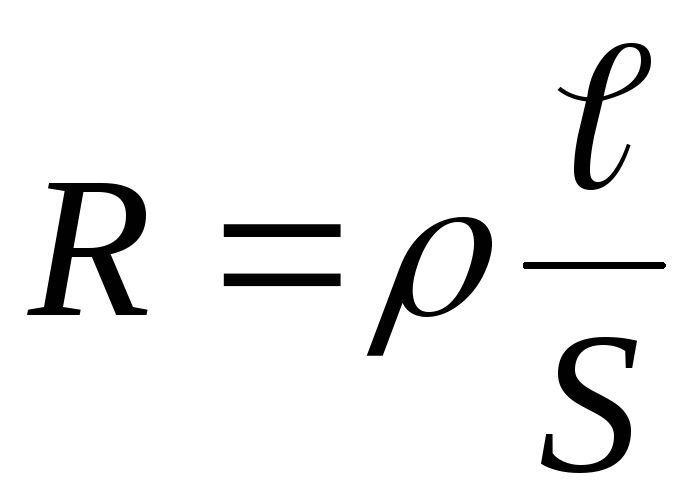(2.4)

где —
удельное сопротивление материала
проводника,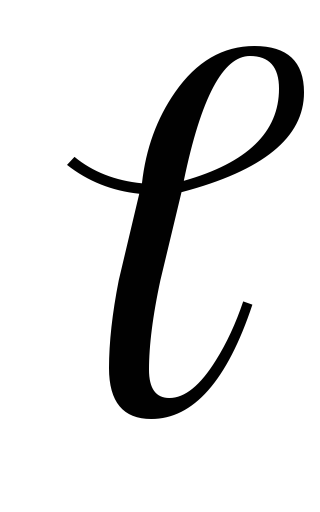,соответственно
длина и площадь сечения проводника.

Подставим (2.4) в
(2.3),

.
(2.5)

Введем понятие
плотности тока j

,
(2.6)

где
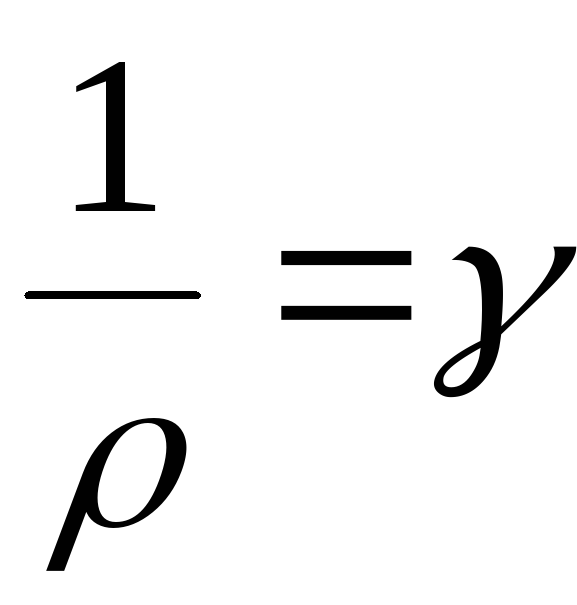удельная проводимость, или
электропроводность, проводника.

Учитывая векторный
характер напряженности электрического
поля
,

(2.7)

Плотность тока

– вектор, совпадающий с вектором
напряжённости
электрического
поля.

Для поддержания
постоянной разности потенциалов на
концах проводника необходимо подключать
его к источнику напряжения, или источнику
тока.(ИТ)

Сторонние силы
действуют на заряды только в источнике
тока. В замкнутой цепи, имеющей источник
тока, помимо сторонних сил действуют
электростатические силы (силы Кулона).

Электрическая
цепь постоянного тока (рис.2.1) включает
сопротивление нагрузки (резистор) R,
сопротивление внутренних деталей
источника тока r
(внутреннее сопротивление), ЭДС ().

Рис. 2.1.

В источнике тока
за счёт его внутренних сил (не Кулоновского
происхождения) разделяются положительные
и отрицательные заряды, которые
скапливаются у его выходных электродов,
и создают разность потенциалов на
клеммах.

Так как к резистору
R
приложена разность потенциалов U,
то, согласно закону Ома, через него
будет идти ток за счёт Кулоновских сил.

(2.8)

По внутренним
деталям ИТ проходит ток

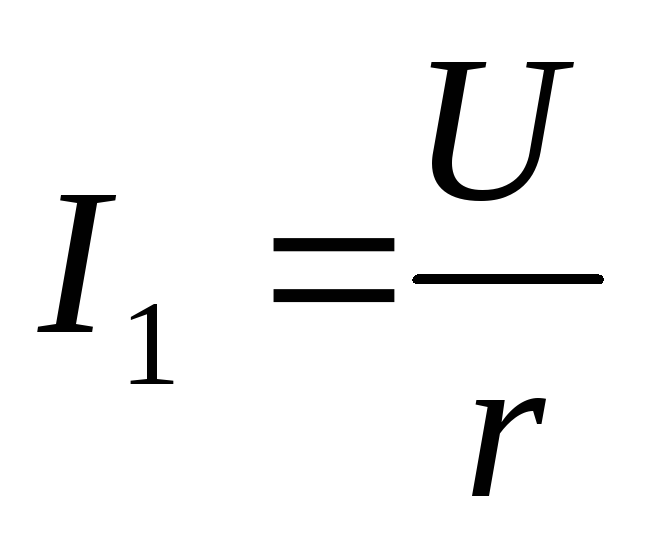(2.9)

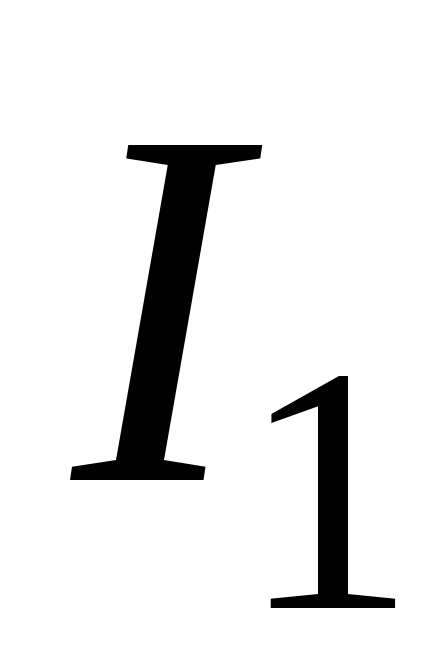Токи
и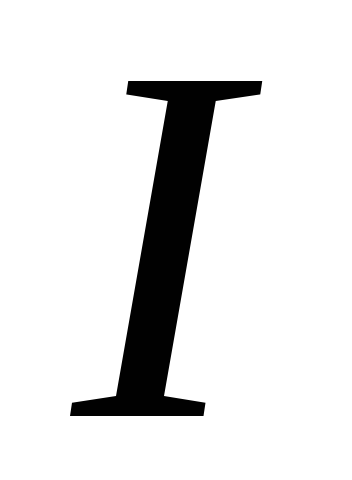приводят
к разряду ИТ и уменьшению количества
положительных и отрицательных зарядов
на его электродах. Сторонние силы
непрерывно восстанавливают количество
этих зарядов на выходных электродах,
т.е. непрерывно восстанавливают
противоположные заряды на электродах
и создают ток,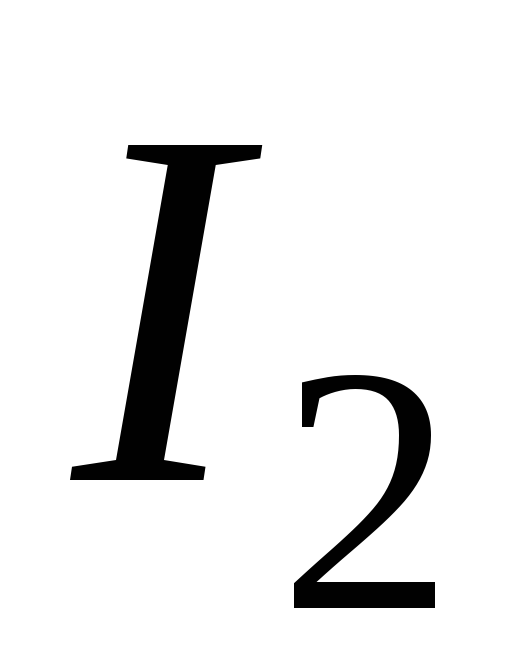
противоположный току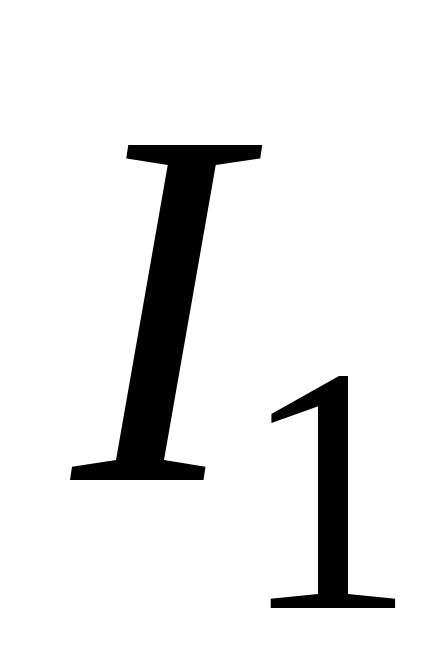(рис.2.2).

В стационарном
процессе, когда токи постоянны

,или

.
(2.10)

Рис. 2.2

Сторонние силы
источника тока, вызывающие ток
,
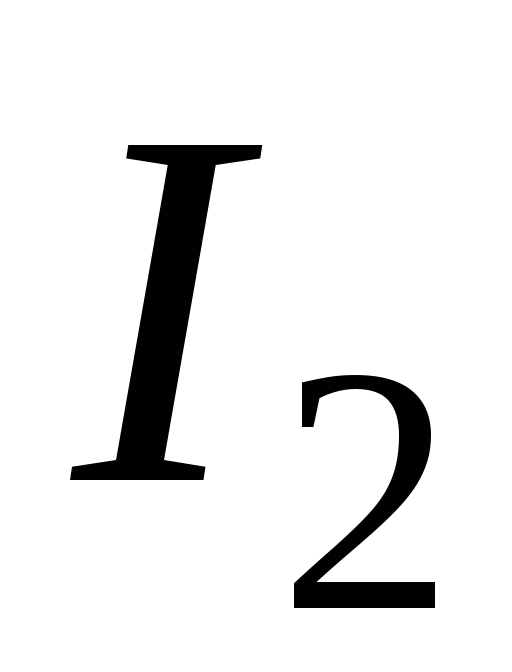появляются в результате действия
химических реакций или других явлений
и называют электродвижущей силой(ЭДС).

Для написания
закона Ома для замкнутой цепи запишем
уравнение (2.10) в виде:

(2.11)

После алгебраических
преобразований

(2.12)

(2.13)

Закон Ома для
замкнутой цепи.

Перепишем
уравнение 2.13 в виде:

(2.14)

где
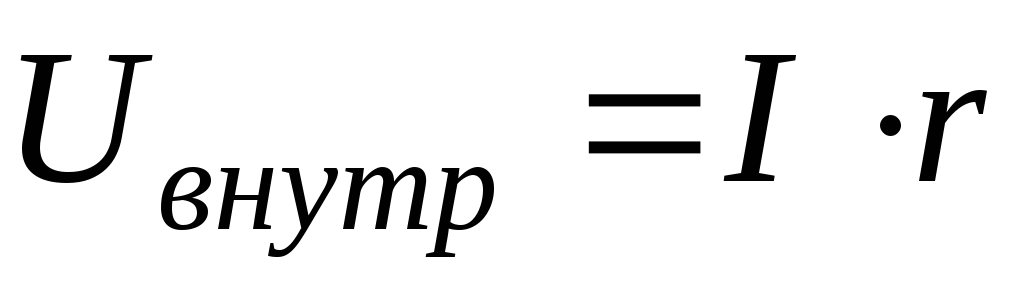падение напряжения на внутренних
деталях источника тока;

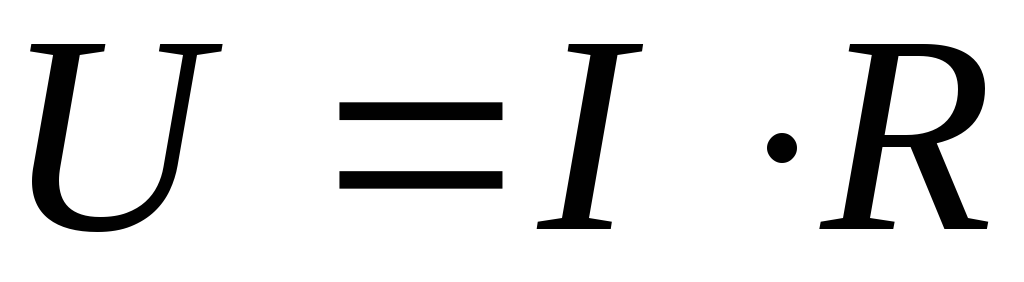падение напряжения
на внешнем сопротивлении R.

Из уравнения
(2.14) следует, что

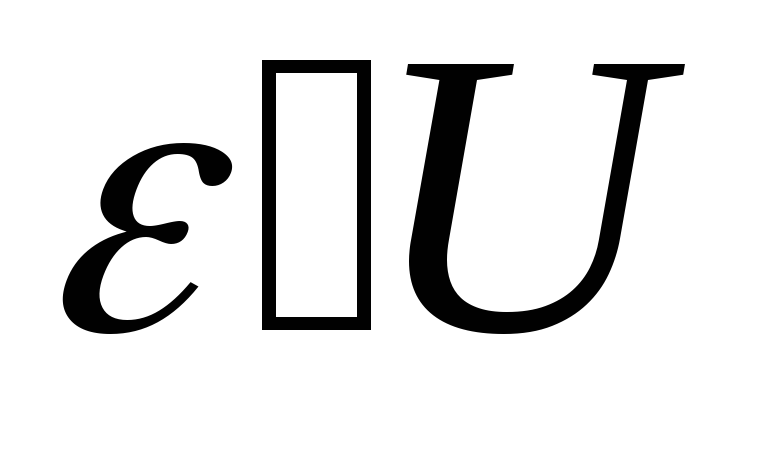(2.15)

Если
то

(2.16)

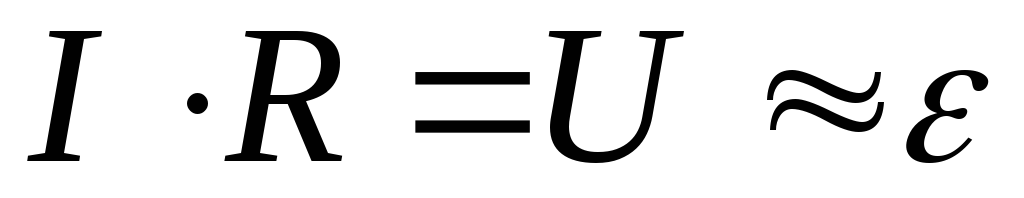иЕсли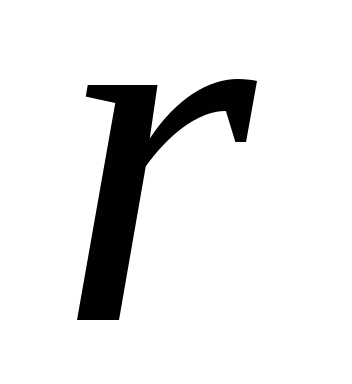соизмеримо сR
(т.е.
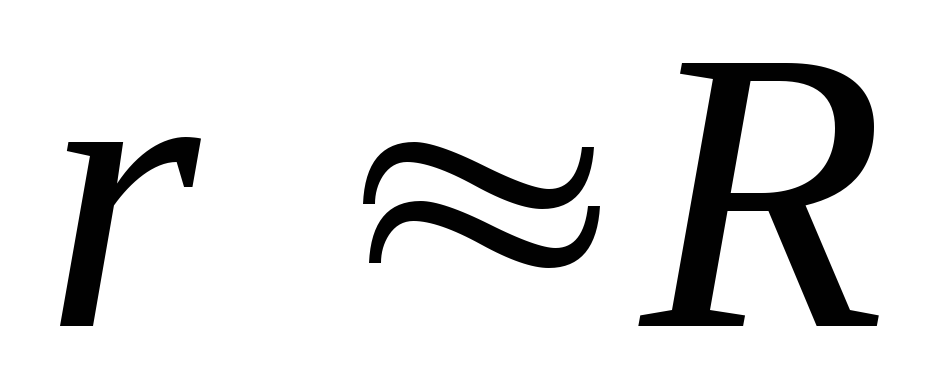), то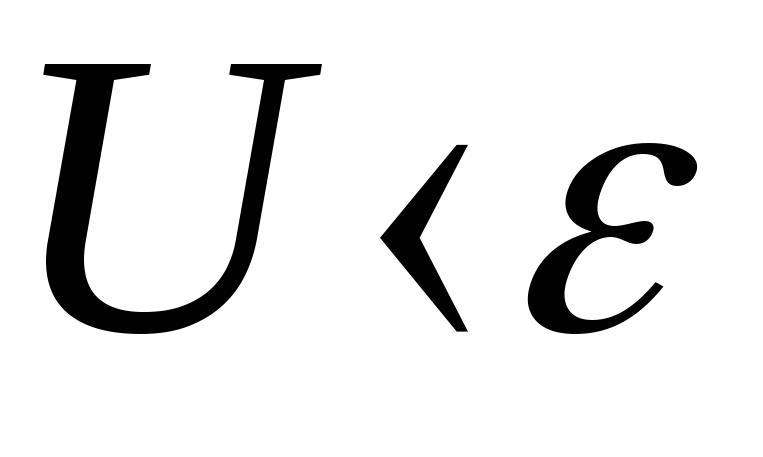(именно поэтому говорят, что источник
тока «подсаживается» при подключении
к нему мощного потребителя тока,
обладающего малымR,
так как:
.

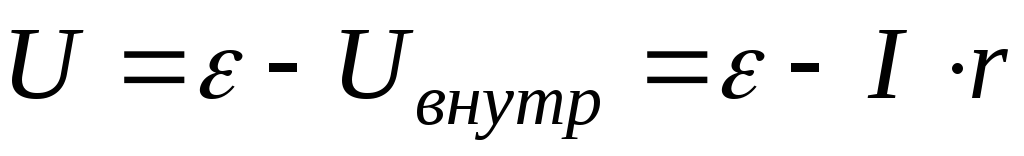Сопротивления
и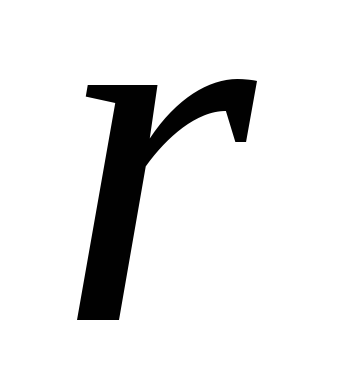в цепи (рис.2.1) включены последовательно,
и следовательно, полное сопротивление

,
( 2.17)

.
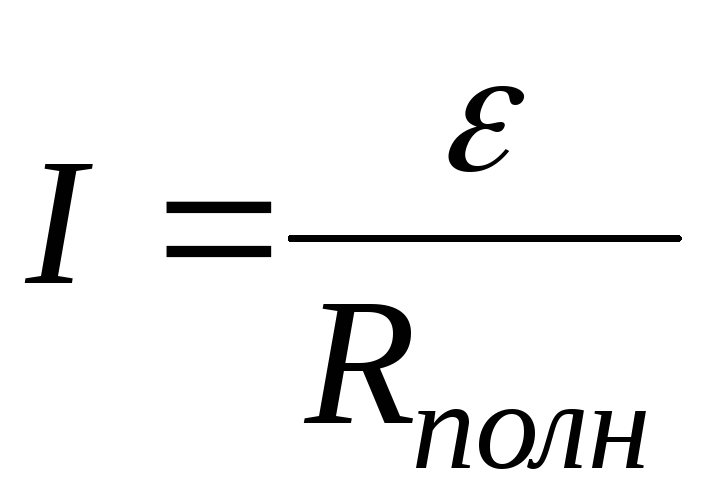( 2.18)

Из уравнения
(2.13) следует, что ток
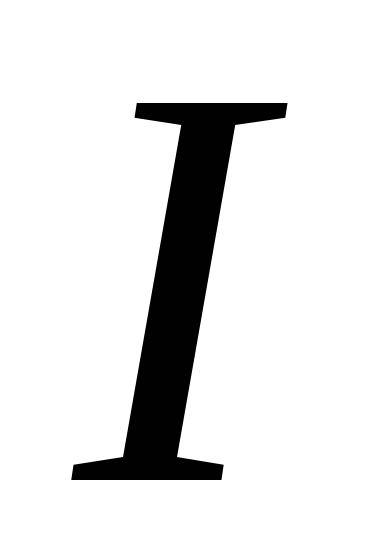у любого источника тока ограничены
из-за его внутреннего сопротивления.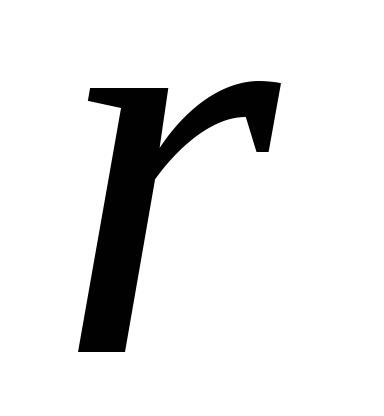
Максимальный ток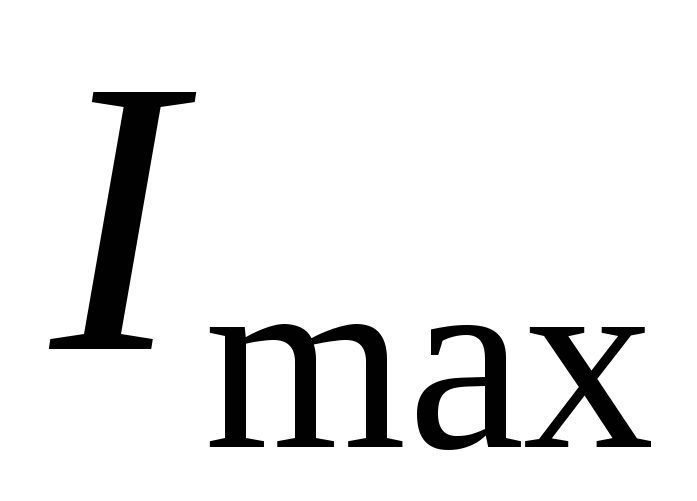возникает в результате короткого
замыкание ()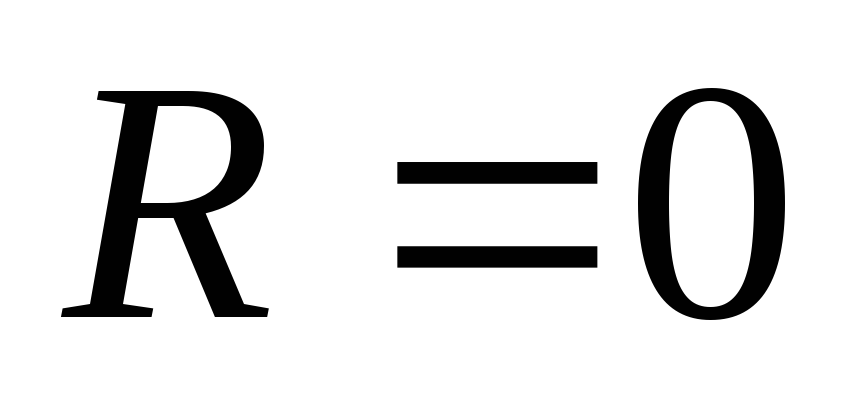

.
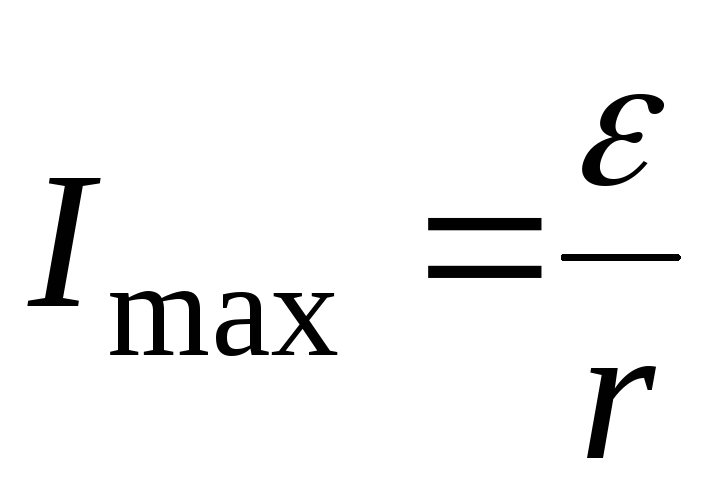( 2.19 )

Например, для
батареи
=1,5
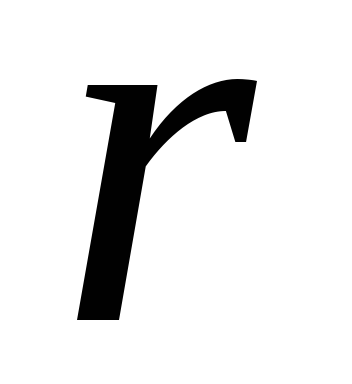В и=0,1
Ом

.

Лекция
5.

1 Энергия системы точечных зарядов

Формулу
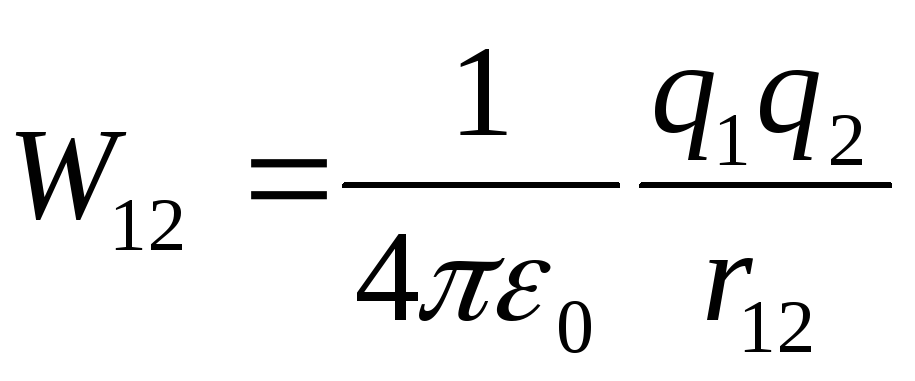можно рассматривать как взаимную
потенциальную энергию зарядов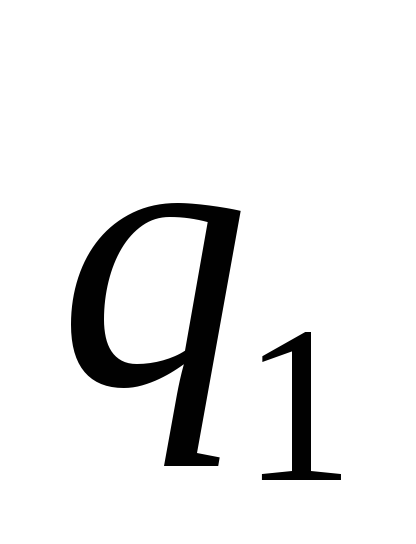и,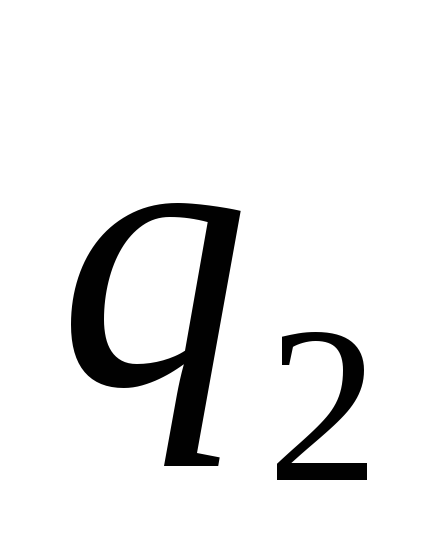
находящихся на расстоянии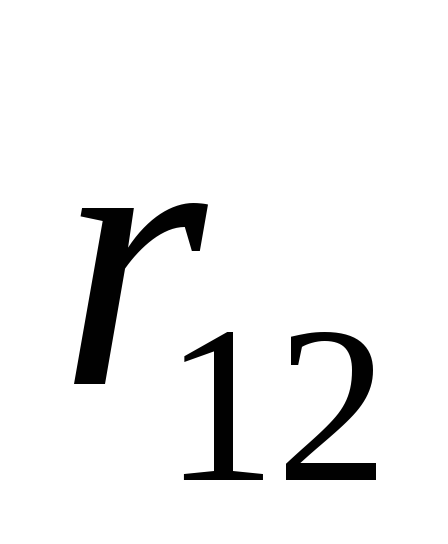(рис.1).

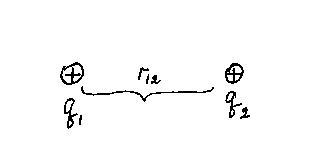
Рис.1

Если мы теперь в поле двух зарядов
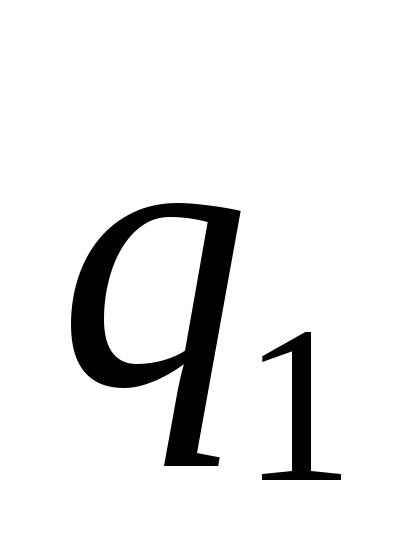и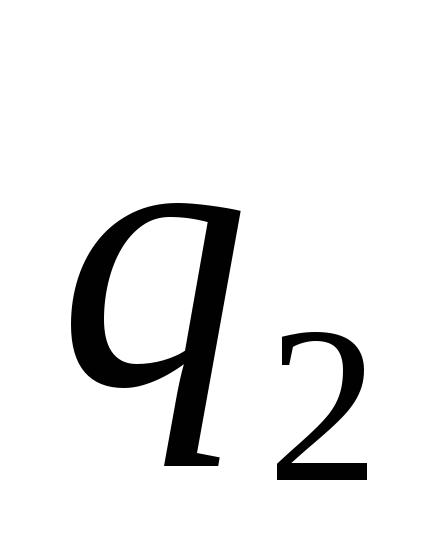внесем
третий заряд,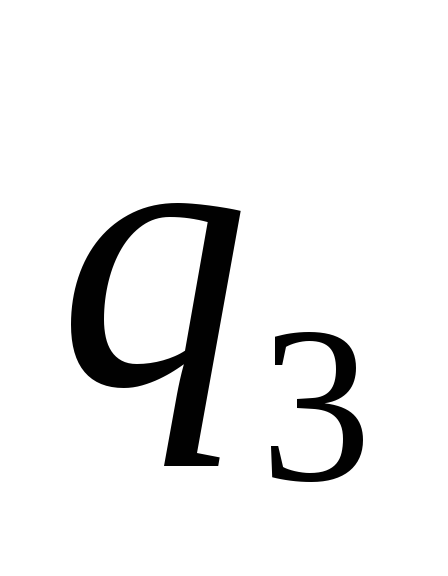
то благодаря свойству аддитивности
энергии взаимодействий, получим:

.

Преобразуем эту сумму следующим образом.
Представим каждое слагаемое
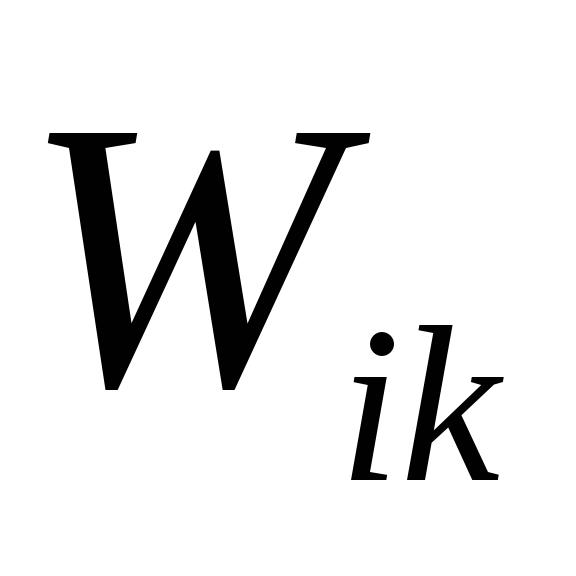в симметричном виде:,
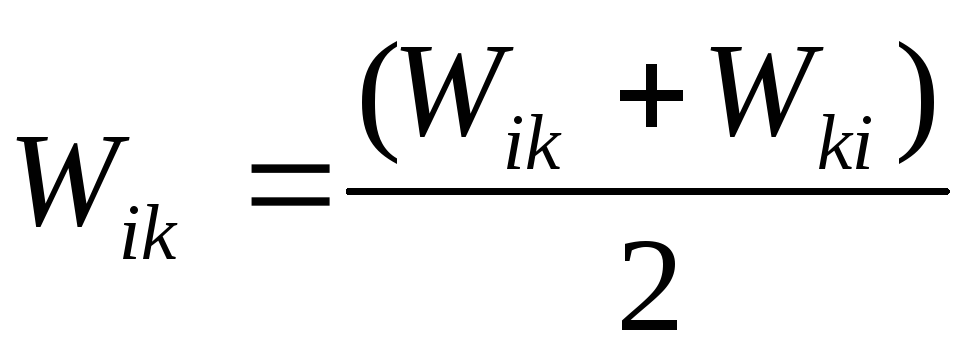поскольку.
Тогда

.

Сгруппируем члены с одинаковыми первыми
индексами:

Каждая сумма в круглых скобках – это
энергия
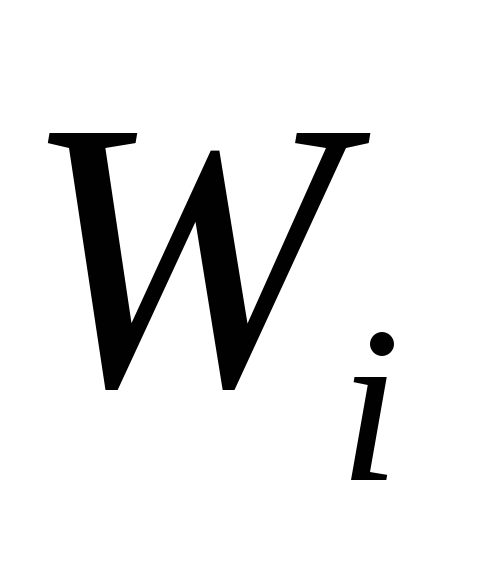взаимодействия-го
заряда с остальными зарядами.

Поэтому можно последнее выражение
переписать так:

Обобщим это выражение на систему,
состоящую из
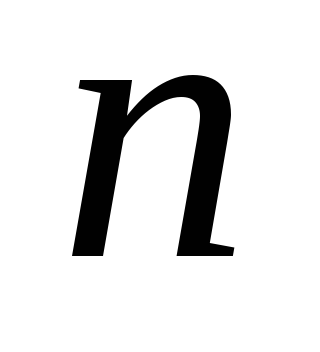точечных зарядов.
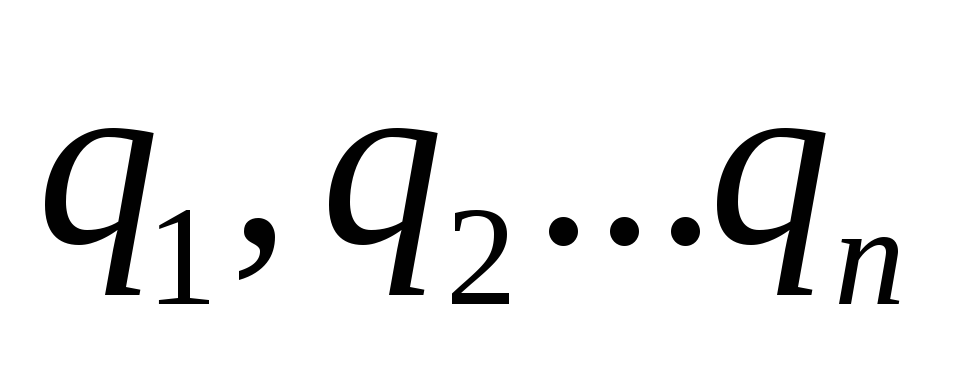Итак, энергия взаимодействия системы
точечных зарядов

(3.1)

Имея в виду, что
,
где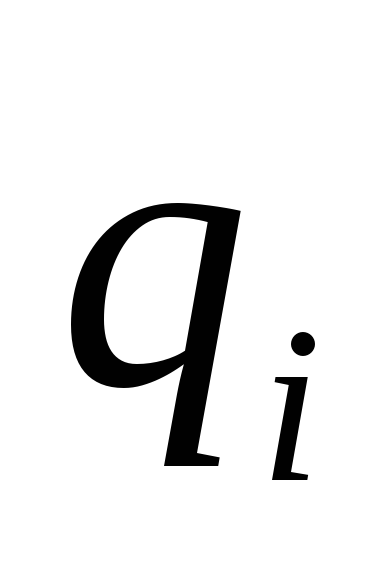-i-ый заряд системы,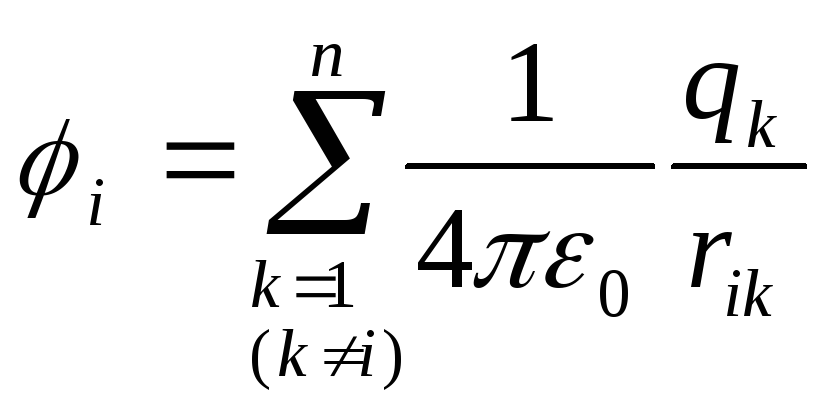— потенциал, создаваемый всеми зарядами,
кроме,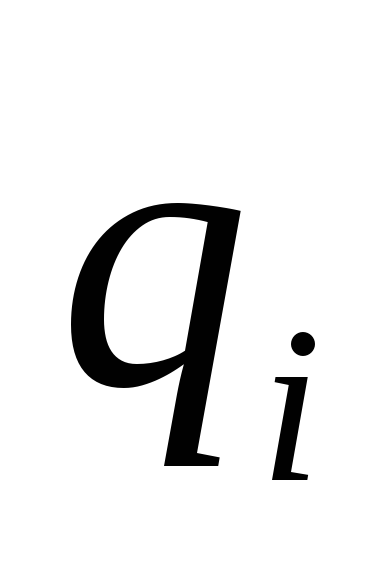
в той точке, где находится заряд,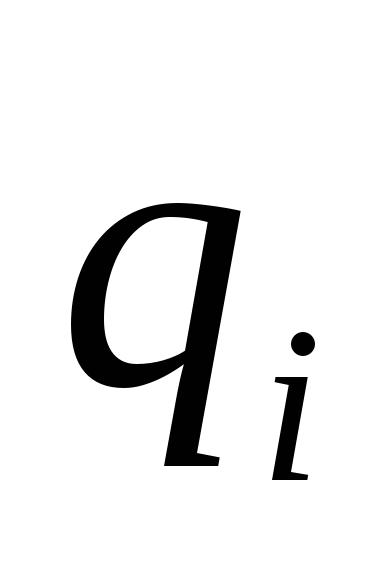
получим окончательное выражение:

(3.2)

Если заряды распределены непрерывно,
то, разлагая систему зарядов на
совокупность элементарных зарядов
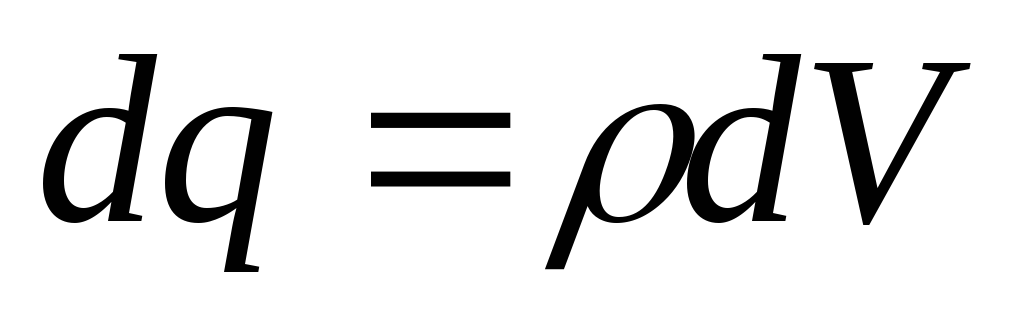и переходя от суммирования в (3.2) к
интегрированию, получаем

,
(3.3)

где
— потенциал, создаваемый всеми зарядами
системы в элементе объемом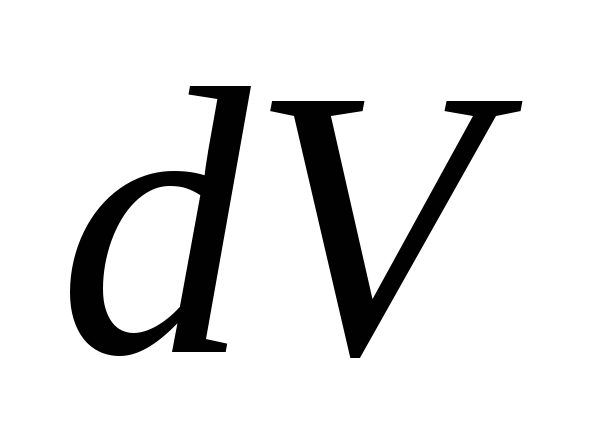.