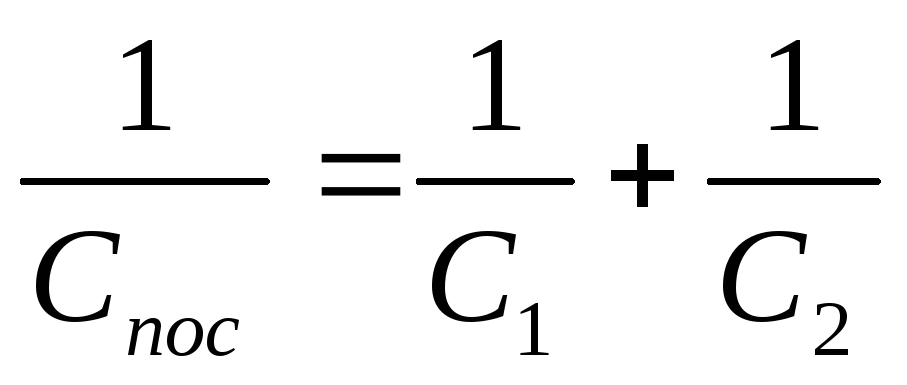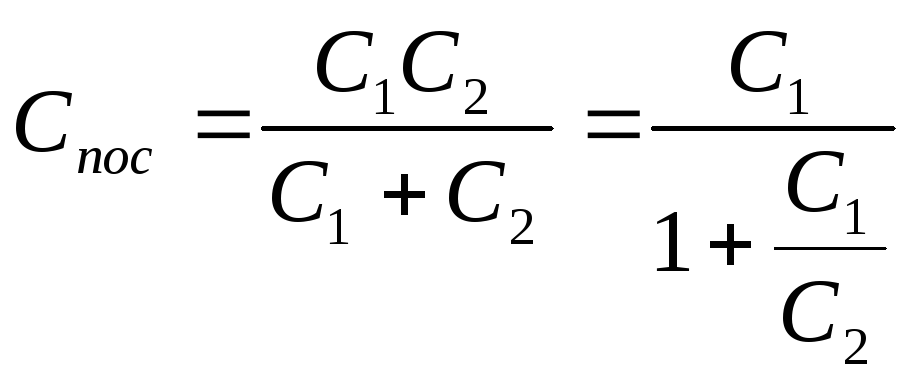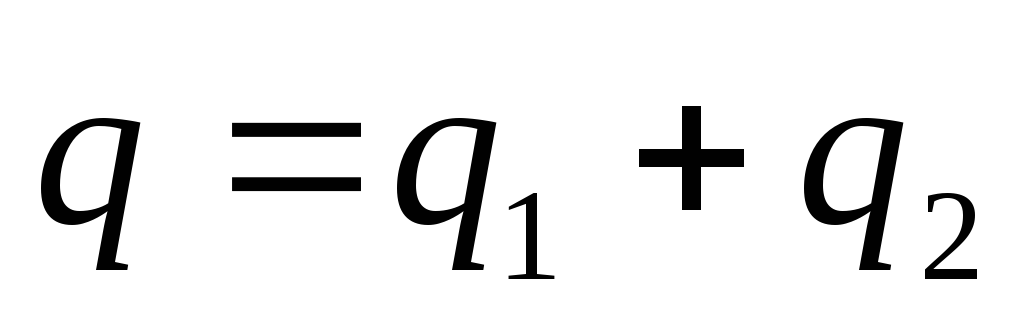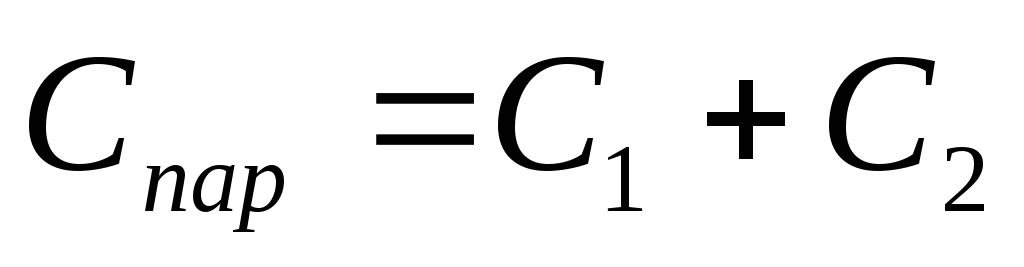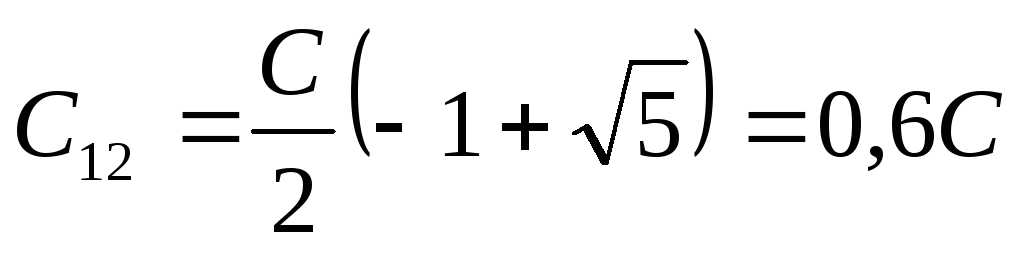Электрический конденсатор

Соединение конденсаторов формулы

1. Последовательное соединение
2. Онлайн калькулятор
3. Смешанное соединение
4. Параллельное соединение
5. Видео

В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.

Последовательное соединение

При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = ic1 = ic2 = ic3 = ic4.

В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Qобщ= Q1 = Q2 = Q3.

Если рассмотреть три конденсатора С1, С2 и С3, соединенные в последовательную цепь, то выясняется, что средний конденсатор С2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.

Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.

Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/Cобщ = 1/C1 + 1/C2 + 1/C3.

Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.

Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.

Параллельное соединение конденсаторов

Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов.

Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что емкость конденсаторов находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, Собщ = С1 + С2 + С3.

Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.

Практические измерения

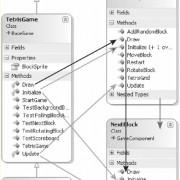
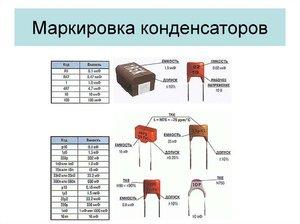Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.

Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.

Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.

Энергия конденсаторов

Конденсатор – прибор для накопления заряда, и проводники, на которых накапливается заряд, создают между собой электрическое поле, а значит, конденсатор обладает некоторой энергией.  Энергия конденсатора, по закону сохранения энергии, должна быть равна работе, выполненной по разделению зарядов.

Как мы уже знаем, работа по перемещению заряда в поле равна:

Здесь:  – заряд;  – напряженность;  – модуль перемещения.

И теперь, если рассмотреть наш случай поля конденсатора, получается, что напряженность  создается одновременно двумя обкладками, и для рассмотрения одной обкладки мы должны записать

Рис. 7. Однородное поле конденсатора

Воспользовавшись теперь формулой связи напряженности и напряжения из прошлого урока:

Формула для энергии конденсатора принимает вид:

Использовав в этой формуле формулу определения емкости конденсатора, можно получить еще две формы записи для энергии:

или

Этот урок завершает тему электростатики. Следующий будет посвящен уже электрическому току.

Дополнение 1. Электроемкость шара.

Для того чтобы оценить насколько велика емкость в 1 Ф, возьмем в качестве накапливающего заряд тела проводящий шар и выведем зависимость его емкости от его размеров.

Из предыдущего урока мы знаем формулу для определения потенциала шара:

Подставим теперь её в определение емкости:

Давайте рассмотрим случай в вакууме или же в воздухе (). Каковы же должны быть размеры шара, чтобы его емкость равнялась 1 Ф?

Для сравнения радиус Земли равен:

Дополнение 2. Соединение конденсаторов.

Иногда не получается найти конденсатор нужной конфигурации, тогда приходится составлять блоки из нескольких конденсаторов. Соединить два или более конденсатора можно двумя различными способами: параллельно или последовательно.

Параллельное соединение (рис. 8):

Рис. 8. Параллельное соединение конденсаторов

Так как выходы источника питания подсоединены одновременно к обкладкам всех конденсаторов, то потенциалы всех обкладок равны, металл является эквипотенциальной поверхностью:

Заряды на обкладках параллельно соединенных конденсаторов суммируются:

Разделив второе равенство на напряжение (любое, так как они равны) и воспользовавшись определением емкости конденсатора, получим:

Последовательное соединение (рис. 9):

Рис. 9. Последовательное соединение конденсаторов

Так как две обкладки соседних конденсаторов являются одной деталью, отрезанной от остальных проводников, по закону сохранения заряда, сумма их зарядов должна оставаться равной нулю, а значит, они равны по модулю, но противоположны по знаку, поэтому:

Падение же напряжения на всем участке складывается из падений напряжения на каждом конденсаторе:

Теперь, разделив второе равенство на заряд (любой, так как они равны) и воспользовавшись определением емкости конденсатора, получим:

Список литературы

1. Тихомирова С.А., Яворский Б.М. Физика (базовый уровень) – М.: Мнемозина, 2012.
2. Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. – М.: Илекса, 2005.
3. Касьянов В.А. Физика 10 класс. – М.: Дрофа, 2010.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Physics.ru (Источник).
2. Электротехника (Источник).
3. Physics.kgsu.ru (Источник).

Домашнее задание

1. Стр. 96-98: № 750–755. Физика. Задачник. 10-11 классы. Рымкевич А.П. – М.: Дрофа, 2013. (Источник)
2. Во сколько раз изменится емкость конденсатора, если листовую слюду заменить парафином той же толщины?
3. Какую площадь должны иметь пластины плоского конденсатора, для того чтобы его электроемкость была равна 1 пФ? Расстояние между пластинами – 0,5 мм.
4. Емкость одного конденсатора больше емкости другого в 4 раза, на какой конденсатор нужно подать большее напряжение, чтобы их энергии стали одинаковыми, во сколько раз больше?
5. *Почему большой заряд не может удержаться на сфере маленького радиуса?

Ёмкость сферического конденсатора.

Сферический
конденсатор представляет собой систему
двух концентрических сфер с радиусамии.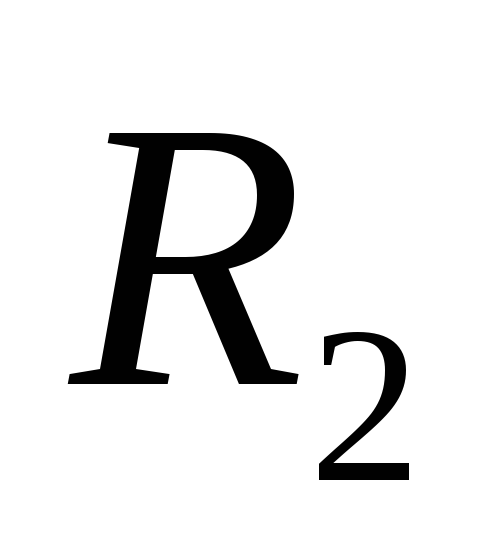
Электрическое поле между обкладками
сферического конденсатора согласно
теореме Гаусса определяется зарядом
внутренней сферы. Напряжение между
обкладками равно:

.

Для ёмкости сферического конденсатора
получаем:

.

Это формула точная.

Если
,
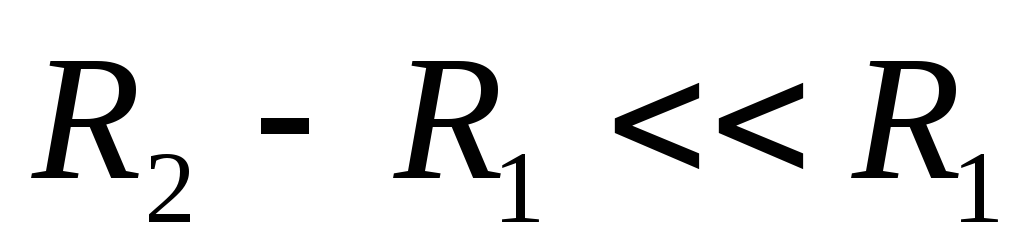полученная формула переходит в выражение
для ёмкости плоского конденсатора.

Ёмкость цилиндрического
конденсатора.

Цилиндрический конденсатор составляет
систему двух коаксиальных цилиндров с
радиусами
и,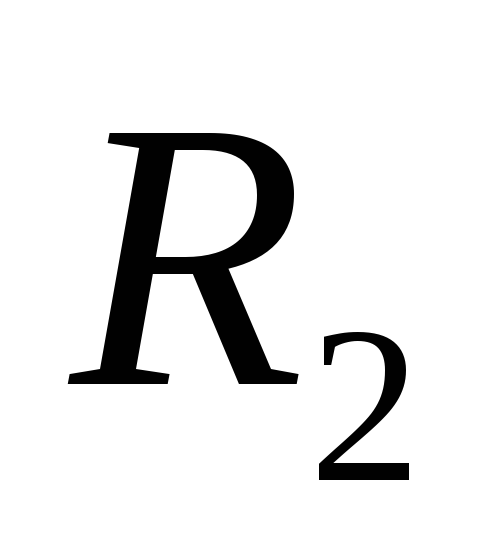
длиной.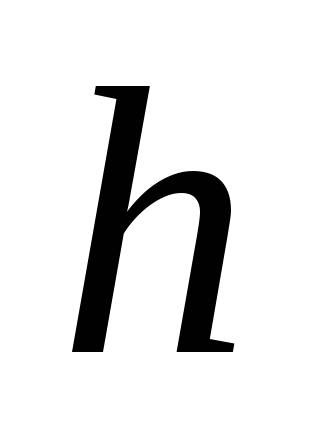

Рассуждая аналогично выводу ёмкости
сферического конденсатора, получаем:

..

Полученная формула является приближенной
и при малом зазоре
переходит в формулу емкости плоского
конденсатора.

Соединение конденсаторов.

В практике для получения необходимых
значений емкости используют соединения
конденсаторов: а) последовательное, б)
параллельное, в) смешанное (см. рисунок).

Ёмкость последовательного
соединения конденсаторов.

Заряды последовательно соединенных
конденсаторов равны
,
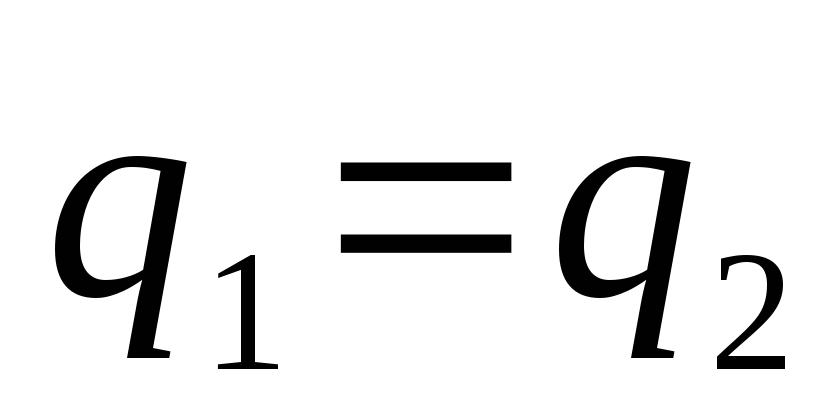а напряжение на батарее.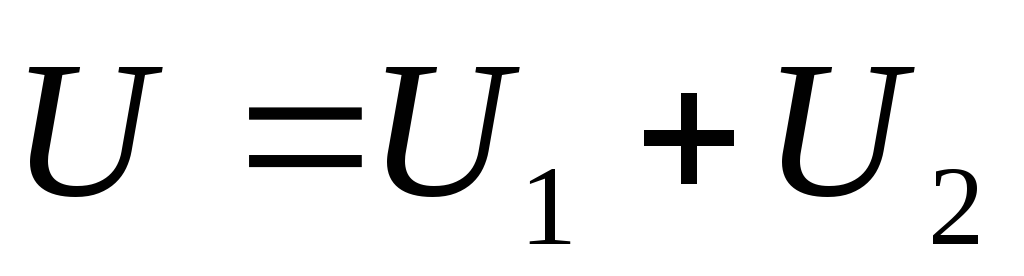
Из определения емкости следует:

или
.

Если
,
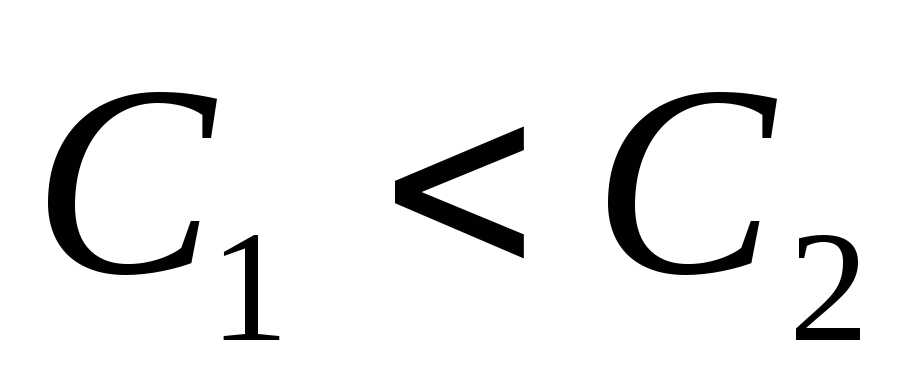то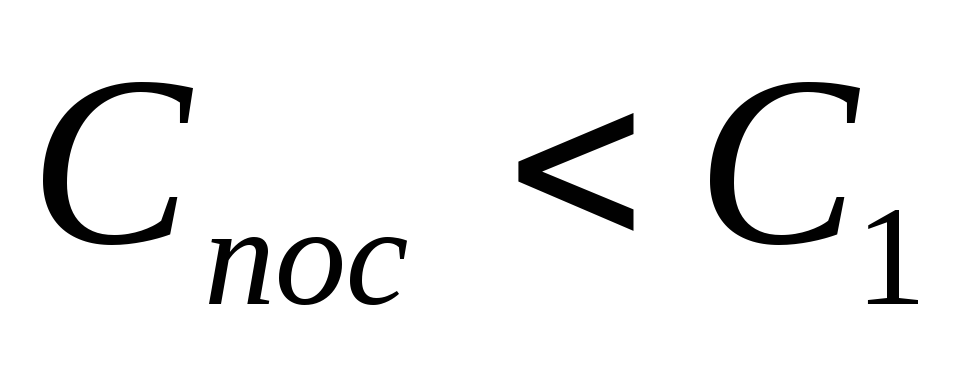(ёмкость последовательного соединения
меньше наименьшей ёмкости в последовательном
соединении).

Для
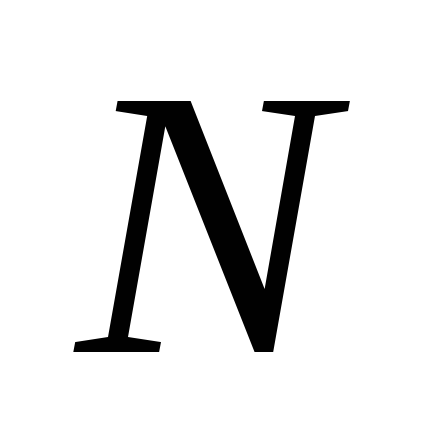последовательно соединенных конденсаторов
емкость вычисляется по формуле:

.

В случае одинаковых конденсаторов:
.

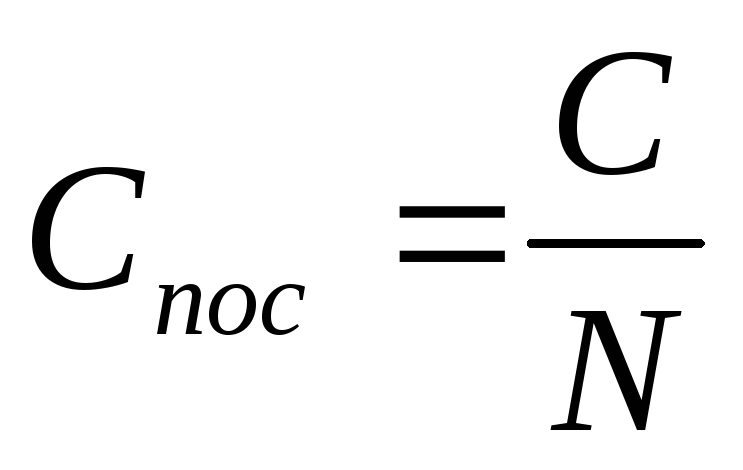Ёмкость параллельного
соединения конденсаторов.

Заряд батареи равен сумме зарядов:

,

а напряжение
.
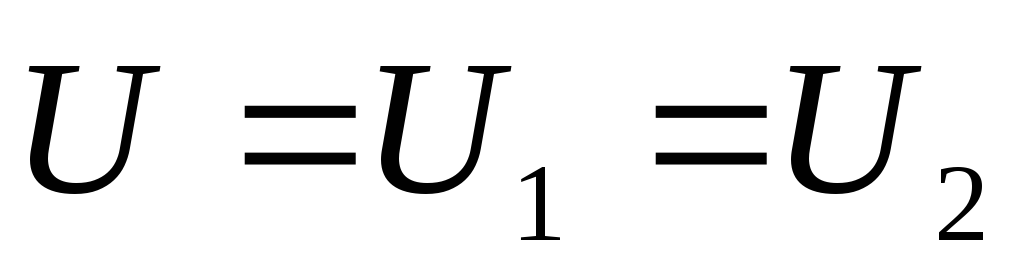По определению емкости получаем:

.

Для
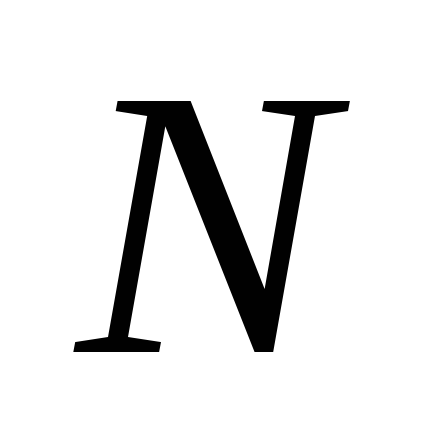параллельно соединенных конденсаторов:.

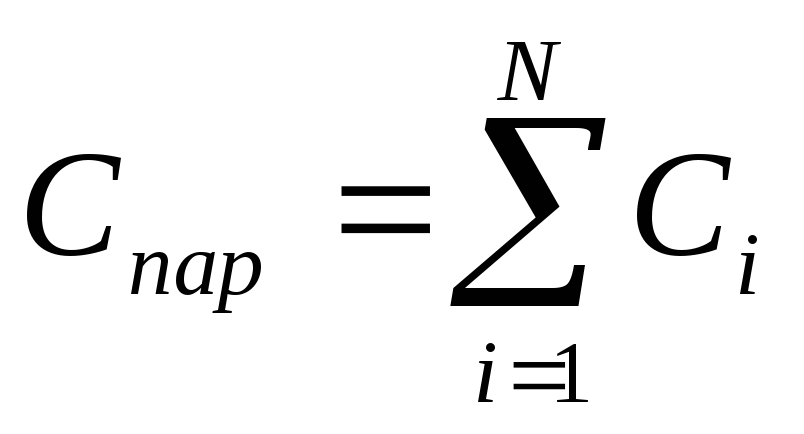В случае одинаковых конденсаторов:
.

Пример.

О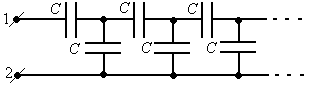ценить
емкость батареи (см. рисунок).

.

Ответ:.

Используя свойство бесконечности можно
представить цепь в виде соединения (см.
рисунок).

Для
расчета ёмкости батареи получаем:

,

.

Откуда:
,
так как,
то.

Лекция 7.

Диэлектрики в электрическом
поле.

Диэлектриками (изоляторами) называют
вещества, не проводящие постоянного
электрического тока. Это означает, что
в диэлектриках отсутствуют «свободные»
заряды, способные перемещаться на
значительные расстояния.

Диэлектрики состоят либо из нейтральных
молекул, либо из ионов, находящихся в
узлах кристаллической решетки. Сами же
молекулы могут быть полярнымиинеполярными.Полярные молекулы
обладают дипольным моментом, у неполярных
молекул дипольный момент равен нулю.

Поляризация.

В электрическом поле диэлектрики
поляризуются. Это явление связано с
появлением в объеме и на поверхности
диэлектрика «связанных» зарядов.
При этом конечный объем диэлектрика
приобретает дипольный момент. Механизм
поляризации связан с конкретным строением
диэлектрика. Если диэлектрик состоит
из неполярных молекул, то в пределах
каждой молекулы происходит смещение
зарядов – положительных по полю,
отрицательных против поля, т.е. молекулы,
приобретают дипольный момент. У
диэлектрика с полярными молекулами в
отсутствии внешнего электрического
поля их дипольные моменты ориентированы
хаотично.

Под
действием электрического поля диполи
ориентируются преимущественно в
направлении поля. Рассмотрим подробнее
этот механизм (см. рисунок). Пара сил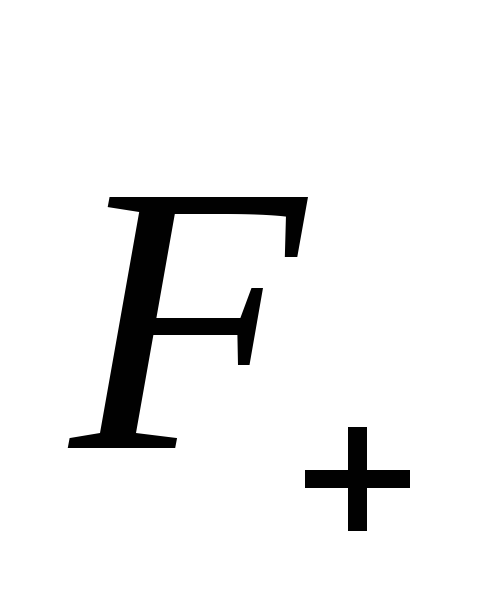и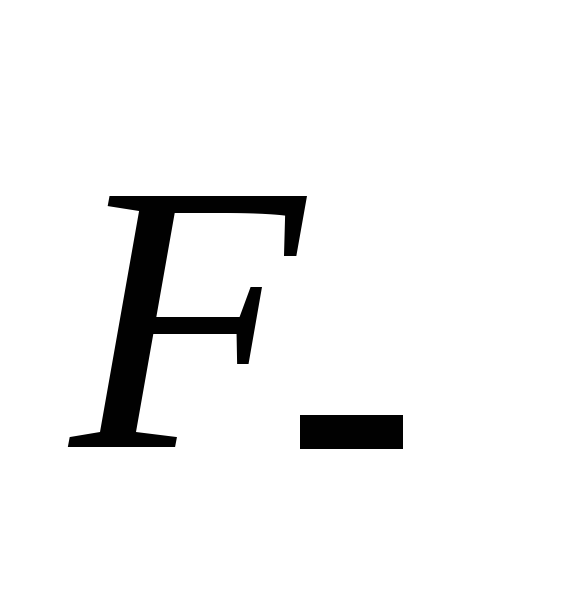создает
вращательный момент равный,
где—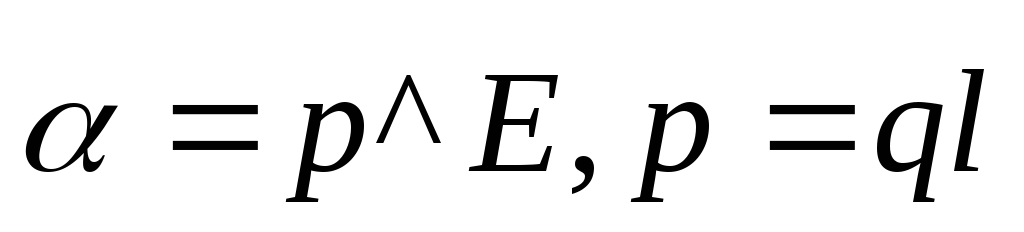
дипольный момент молекулы. Этот момент
стремится ориентировать диполь вдоль
поля. В ионных кристаллах под действием
электрического поля все положительные
ионы смещаются по полю, отрицательные
– против поля. Отметим, что смещение
зарядов очень малы даже по сравнению с
размерами молекул. Это связано с тем,
что напряженность внешнего электрического
поля обычно много меньше напряженности
внутренних электрических полей в
молекулах.

Отметим, что существуют диэлектрики,
поляризованные даже при отсутствии
внешнего поля (электреты, сегнетоэлектрики).
Мы остановимся на рассмотрении только
однородных диэлектриков, в которых
отсутствует остаточная поляризация, а
объемный и «связанный» заряд всегда
равен нулю
.

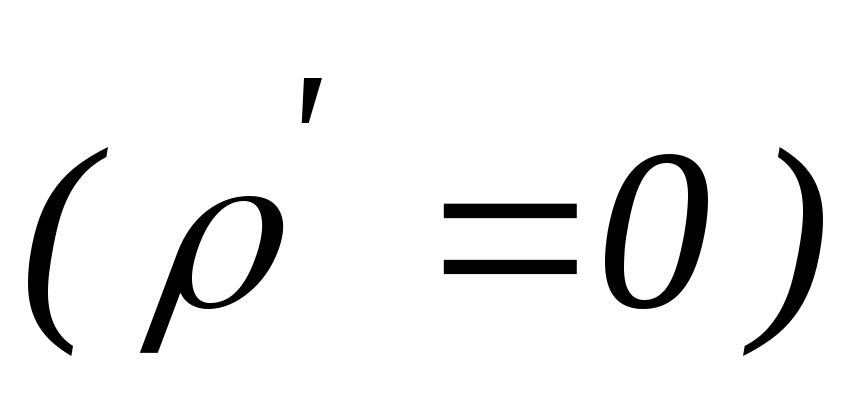Где и как используются конденсаторы

Перед тем как начать рассказывать об области применения конденсаторов, вспомним, что конденсатор это — две пластины, разделенные диэлектриком. Поэтому ток через конденсатор (в первом приближении) идти не может. Однако в цепи с конденсатором могут происходить процессы заряд и разряда. И во время этих процессов в цепи будут протекать токи заряда или разряда.

Таким образом, если переменное напряжение будет приложено  к цепи с конденсатором, в ней будет протекать переменный ток. Поэтому конденсатор можно охарактеризовать такой величиной как емкостное сопротивление (обозначается в технической литературе как Хс).

Емкостное сопротивление зависит от ёмкости конденсатора и частоты приложенного напряжения. Чем ёмкость и частота больше, тем меньше емкостное сопротивление. На этих эффектах основано применение конденсаторов в схемах фильтрации источников питания.

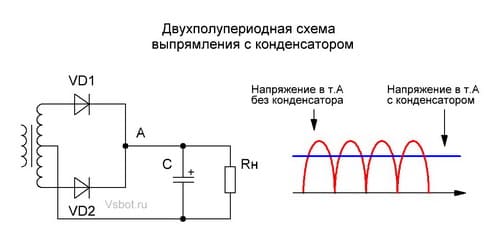
В компьютерных блоках питания для получения постоянных напряжений +3,3, +5, и +12 В используется двухполупериодная схема выпрямление с двумя диодами и фильтрующим конденсатором. Без конденсатора на нагрузке будет пульсирующее напряжение одной полярности.

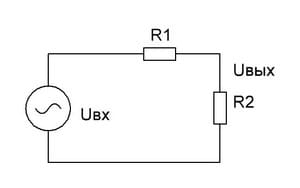Источник постоянного напряжения можно представить в виде эквивалентной схемы из генератора и двух сопротивлений, где R1 — это внутреннее сопротивление выпрямителя, а R2 — емкостное сопротивление конденсатора.

Генератор – это сумма постоянного и переменного напряжений (пульсирующее напряжение содержит в себе постоянную и переменную составляющую).

Таким образом, сигнал с генератора подается на частотно-зависимый делитель напряжения. Выходной сигнал снимается с нижнего плеча (конденсатора). Для постоянного напряжения сопротивление конденсатора очень велико, гораздо больше сопротивления выпрямителя. Поэтому уменьшения постоянного напряжения не происходит.

Для переменного напряжения сопротивления конденсатора очень мало, гораздо меньше сопротивления выпрямителя, поэтому происходит сильное ослабление переменной составляющей.

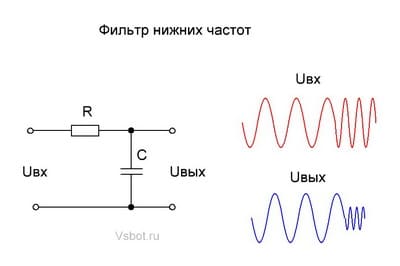Вообще, такая комбинация активного сопротивления и конденсатора называется фильтром нижних частот, который пропускает постоянную составляющую и какой-то диапазон низких частот.

Чем выше частота входного переменного напряжения, тем сильнее оно ослабляется.

Так как необходимо сильное подавление пульсаций переменного напряжения, то используется электролитические конденсаторы большой емкости.

Назначение керамических SMD конденсаторов на материнской плате — подавлять высокочастотные помехи, возникающие при переключении транзисторов в микросхемах. Таким образом, электролитические конденсаторы фильтруют относительно низкочастотные помехи и пульсации, а керамические  — более высокочастотные.

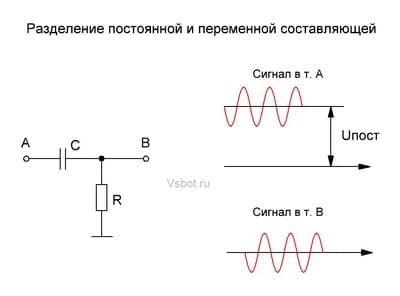Приведем еще один пример разделения переменной и постоянной составляющей. Пусть в схеме на рисунке сигнал в точке А будет иметь постоянную составляющую 5 В и переменную амплитудой 2 В.

После конденсатора,  в точке В будет уже только переменная составляющая той же амплитудой 2 В (если емкостное сопротивление конденсатора мало для такой частоты). Интересно, не правда ли?

По существу, это тоже частотно-зависимый делитель напряжения, где в виде нижнего плеча выступает сопротивление нагрузки. Такую комбинацию называют фильтром верхних частот, который не пропускает постоянную составляющие и низкие частоты, так как в емкостное сопротивление будет для них большим.

Заканчивая, отметим маленькую деталь: так как максимальное напряжение на конденсаторе будет равно сумме постоянной и переменной составляющей, его рабочее напряжение должно быть не менее этой величины.

Купить конденсаторы можно

Продолжение следует.

Электроемкость

На предыдущих уроках мы знакомились с элементарными электрическими понятиями и принципами, в частности, мы говорили об электризации – явлении перераспределения заряда. Разговор о более глубоком исследовании этого явления начнем с опыта.

Изначально пусть нам даны две разные по размеру изолированные банки, подключенные к электроскопу (рис. 1):

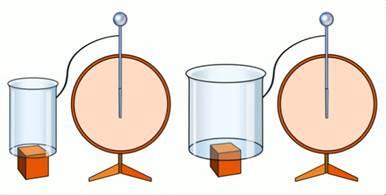
Рис. 1

Теперь к каждой из банок поднесли одинаково заряженное тело. Естественно, с каждой банкой произойдет процесс электризации, и стрелки обоих электроскопов разойдутся. Однако оказалось, что электроскоп большей банки показал меньшее отклонение (рис. 2):

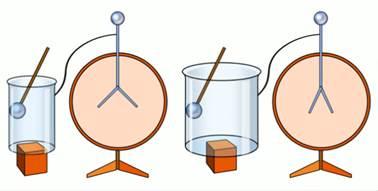
Рис. 2

Данный опыт доказывает, что различные тела электризуются одним и тем же зарядом по-разному (конкретно большая банка одним и тем же зарядом зарядилась до меньшего потенциала). И существует некоторая величина, которая показывает способность тела накапливать электрический заряд. Собственно, о ней и пойдет речь.

Определение. Электроемкость (емкость) – величина, равная отношению заряда переданного проводнику к потенциалу этого проводника.

Здесь:  – емкость;  – переданный заряд;  – потенциал, до которого зарядился проводник.

Физика ёмкостных характеристик

Устройства, обладающие способностью хранения энергии в форме электрического заряда и производящие при этом разность потенциалов, называют конденсаторами. В простейшем виде они состоят из двух или более параллельных проводящих пластин, находящихся на небольшом расстоянии друг от друга, но электрически разделённых либо воздухом, либо каким-либо другим изоляционным материалом, например, вощёной бумагой, слюдой, керамикой, пластмассой или специальным гелем.

Если подключить к пластинам источник напряжения, то одна из них получит избыток электронов, а на другой сформируется их дефицит. Ионы и электроны на каждой из этих пластин притягиваются друг к другу, но благодаря диэлектрическому барьеру они не соединяются, а накапливаются на плоскостях проводников. В результате первая пластина (электрод) окажется заряженной отрицательно, а вторая — положительно. Неподвижные заряды создают постоянное электрическое поле, теоретически сохраняемое неограниченное количество времени в незамкнутой электрической цепи.

Поток электронов на пластины называется зарядным током, продолжающим присутствовать до тех пор, пока напряжение на пластинах не сравняется с приложенным. В этот момент конденсатор считается полностью заряженным, то есть зарядов на пластинах становится так много, что они отталкивают вновь поступающие. При подключении к заряженному устройству нагрузки электроны и ионы находят новый путь друг к другу. В этом случае конденсатор работает как источник тока до момента потери разности потенциалов на электродах.

Способность конденсатора хранить заряд Q (измеряется в кулонах) называют ёмкостью. Чем больше площадь пластин и меньше расстояние между ними (благодаря усилению эффекта притяжения зарядов между обкладками), тем большая ёмкость устройства. Степень приближения пластин ограничивается способностью диэлектрика сопротивляться разрядке пробоем между ними. Таким образом, три характеристики определяют производительность конденсатора:

• геометрия пластин;
• расстояние между ними;
• диэлектрический материал между пластинами.

Идея суперконденсатора

Электричество — чрезвычайно универсальный вид энергии, обладающий одним недостатком — его трудно саккумулировать быстро. Химические батареи способны сохранять большое количество энергии, но требуют нескольких часов для полной зарядки. Этого недостатка лишены конденсаторы — они могут заряжаться практически мгновенно. Но их ёмкость не позволяет хранить большое количество энергии, поэтому весьма заманчивой выглядит идея суперконденсатора, сочетающего лучшие качества химических и электростатических накопителей электричества.

Несмотря на функциональную схожесть, аккумуляторные батареи и конденсаторы устроены совершенно по-разному. Гальванические элементы работают на принципе высвобождения электрической энергии во время химической реакции веществ внутри них. При истощении запаса активных реагентов они прекращают генерировать разность потенциалов и для нового цикла требуют инициирования током обратных химических реакций для восстановления активных веществ. Основные недостатки аккумуляторов по сравнении и конденсаторами:

• непродолжительный жизненный цикл;
• невысокая удельная мощность;
• узкий диапазон температур зарядки и разрядки;
• неспособность быстро отдать весь запас энергии.

Тем не менее обычные конденсаторы не используются в качестве активных источников напряжения из-за низкой ёмкости. Теоретические и практические суперконденсаторы (ультраконденсаторы) отличаются от обычных крайне высокой ёмкостью при большой плотности хранимой энергии, что позволяет их рассматривать как альтернативу химическим элементам.

Крупнейшие коммерческие устройства обладают ёмкостью до нескольких тысяч фарад, но их возможности всё равно несопоставимы с аккумуляторами, поэтому подобные устройства используются для хранения зарядов в течение относительно короткого периода времени. Они нашли широкое применение в качестве электрических эквивалентов механических маховиков, чтобы сглаживать напряжение источников питания, например, в ветровых турбинах или рекуперативных тормозных системах электрических транспортных средств.

Первые ультраконденсаторы появились в середине прошлого века и обладали не очень впечатляющими ёмкостями. С тех пор прогресс в совершенствовании материалов привёл к утоньшению диэлектрического слоя до одной молекулы, что позволило создавать устройства с выдающимися характеристиками. Дальнейшее развитие наноиндустрии стало основой для фундаментальных перемен в накоплении электричества. Возможно, в скором времени экологически опасные и капризные химические аккумуляторы заменят суперконденсаторы на основе молекулярно структурированных пластин и диэлектрического слоя.

Как устроен конденсатор

Вообще говоря, конденсатор накапливает на обкладках заряд (множество элементарных частиц, каждая из которых обладает элементарным зарядом). Чем больший заряд накоплен, тем большая запасена энергия. Ёмкость конденсатора зависит также и от вида диэлектрика.

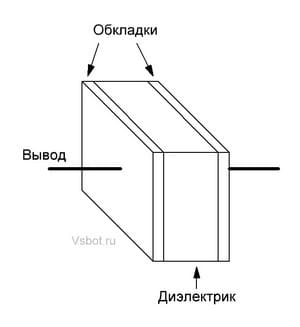Две пластины, разделенные тонким воздушным слоем (воздух — тоже диэлектрик), обладают очень небольшой емкостью, и в таком виде конденсаторы не используются.

С помощью специальных материалов и технологических ухищрений научились достаточно большую ёмкость втискивать в очень небольшой объём.

Самый характерный пример — электролитические конденсаторы.

В них две металлические обкладки в виде длинных полос (чаще всего из алюминиевой фольги) разделены слоем бумаги, пропитанной электролитом.

Электролит вызывает образование тонкой пленки оксида (окисла), которая является хорошим диэлектриком.

Поэтому электролитические конденсаторы называют ещё оксидными. Полосы сворачивают и помещают в цилиндрический алюминиевый корпус.

Раньше выводы конденсаторов делали из меди – как из материала с высокой электропроводностью. Теперь же их нередко делают из более дешевых сплавов на основе железа. В этом можно убедиться, если поднести к ним магнит. Фирмачи научились экономить!

В керамических конденсаторах диэлектриком служит пластинка из керамики, а обкладками – напыленные на керамику пленки металлических сплавов.

Параллельное соединение конденсаторов.

Если группа конденсаторов включена в цепь таким обра­зом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).

Рисунок 2. Параллельное соединение конденсаторов.

При заряде группы конденсаторов, соединенных параллель­но, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количе­ство электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из кон­денсаторов, так как заряд каждого их конденсаторов проис­ходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединен­ных конденсаторов можно рассматривать как один эквива­лентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.

Обозначим суммарную емкость соединенных в батарею конденсаторов бук­вой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:

Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и во­обще при любом числе конденсаторов.
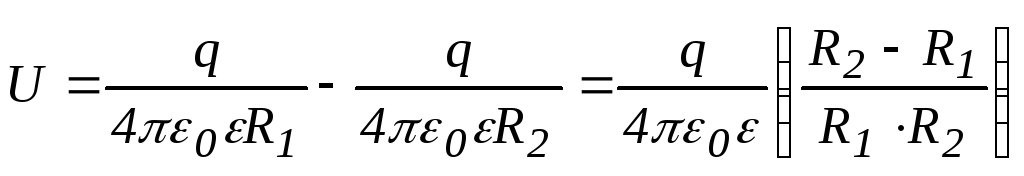
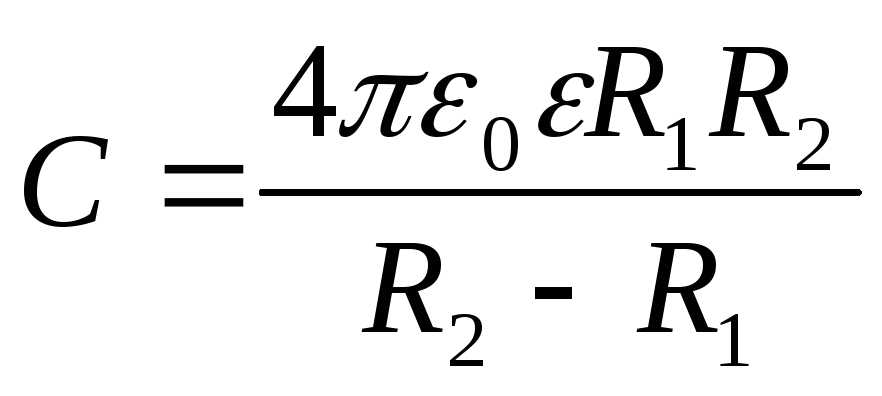
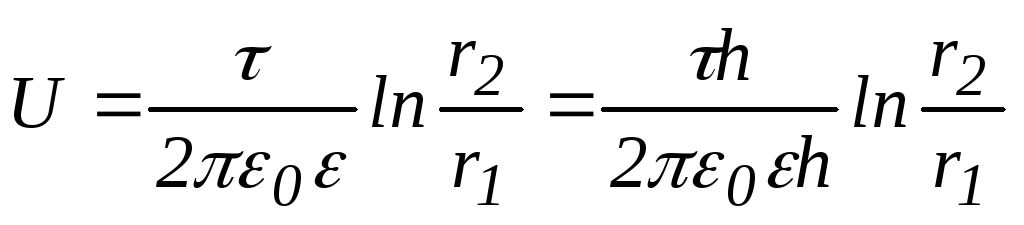
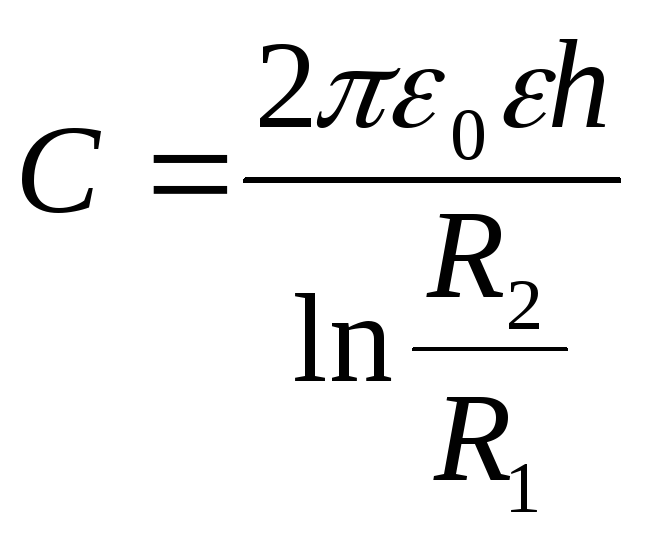