Электрическая катушка описание и применение

Содержание:

Глава 1. Электродинамика Магнитное поле
Теоретическое обоснование
Ресчет катушек индуктивности однослойных, цилиндрических
Методы расчета индуктивностей
Индуктивность длинного прямого проводника
Физика для средней школы
Индуктивность. Явление самоиндукции
Индуктивность тороидальной катушки катушки с кольцевым сердечником
Разновидности катушек индуктивности
Применение катушек индуктивности
Таблица индуктивностей
Применение в технике

Глава 1. Электродинамика Магнитное поле

Самоиндукция
является важным частным случаем
электромагнитной индукции, когда
изменяющийся магнитный поток, вызывающий
ЭДС индукции, создается током в самом
контуре. Если ток в рассматриваемом
контуре по каким-то причинам изменяется,
то изменяется и магнитное поле этого
тока, а, следовательно, и собственный
магнитный поток, пронизывающий контур.
В контуре возникает ЭДС самоиндукции,
которая согласно правилу Ленца
препятствует изменению тока в контуре.

Собственный
магнитный
поток Φ,
пронизывающий контур или катушку с
током, пропорционален силе тока I:

Φ
= LI.

Коэффициент
пропорциональности L
в этой формуле называется коэффициентом
самоиндукции
или индуктивностью
катушки. Единица индуктивности в СИ
называется генри
(Гн). Индуктивность контура или катушки
равна 1 Гн, если при силе постоянного
тока 1 А собственный поток равен 1 Вб:

1 Гн = 1 Вб / 1 А.

В
качестве примера рассчитаем индуктивность
длинного соленоида, имеющего N
витков, площадь сечения S
и длину l.
Магнитное поле соленоида определяется
формулой (см. § 1.17)

B
= μIn,

где
I
– ток в соленоиде, n = N / e
– число витков на единицу длины соленоида.

Магнитный
поток, пронизывающий все N
витков соленоида, равен

Φ
= B·S·N
= μn2SlI.

Следовательно, индуктивность соленоида
равна

L
= μn2Sl
= μn2V,

где
V
= Sl
– объем соленоида, в котором сосредоточено
магнитное поле. Полученный результат
не учитывает краевых эффектов, поэтому
он приближенно справедлив только для
достаточно длинных катушек. Если соленоид
заполнен веществом с магнитной
проницаемостью μ,
то при заданном токе I
индукция магнитного поля возрастает
по модулю в μ раз (см. §
1.17);
поэтому индуктивность катушки с
сердечником также увеличивается в μ
раз:

L_μ
= μL
= μμn2V.

ЭДС
самоиндукции,
возникающая в катушке с постоянным
значением индуктивности, согласно
формуле
Фарадеяравна

ЭДС
самоиндукции прямо пропорциональна
индуктивности катушки и скорости
изменения силы тока в ней.

Магнитное
поле обладает энергией. Подобно тому,
как в заряженном конденсаторе имеется
запас электрической энергии, в катушке,
по виткам которой протекает ток, имеется
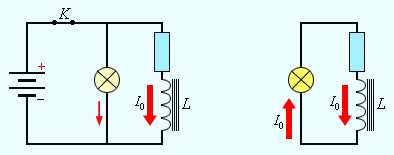
запас магнитной энергии. Если включить
электрическую лампу параллельно катушке
с большой индуктивностью в электрическую
цепь постоянного тока, то при размыкании
ключа наблюдается кратковременная
вспышка лампы (рис. 1.21.1). Ток в цепи
возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при
этом в электрической цепи, является
магнитное поле катушки.

Рисунок
1.21.1.

Магнитная
энергия катушки. При размыкании ключа
K
лампа ярко вспыхивает.

Из
закона сохранения энергии следует, что
вся энергия, запасенная в катушке,
выделится в виде джоулева тепла. Если
обозначить через R
полное сопротивление цепи, то за время
Δt
выделится количество теплоты ΔQ = I2RΔt.

Ток в цепи равен

Выражение
для ΔQ
можно записать в виде

ΔQ
= –LIΔI
= –Φ(I)ΔI.

В
этом выражении ΔI I
до нуля. Полное количество теплоты,
выделившейся в цепи, можно получить,
выполнив операцию интегрирования в
пределах от Iдо 0. Это дает

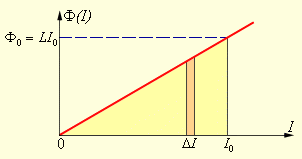
Эту
формулу можно получить графическим
методом, изобразив на графике зависимость
магнитного потока Φ(I)
от тока I
(рис. 1.21.2). Полное количество выделившейся
теплоты, равное первоначальному запасу
энергии магнитного поля, определяется
площадью изображенного на рис. 1.21.2
треугольника.

Рисунок
1.21.2.

Вычисление
энергии магнитного поля.

Таким
образом, энергия W_м
магнитного поля катушки с индуктивностью
L,
создаваемого током I,
равна

Применим
полученное выражение для энергии катушки
к длинному соленоиду с магнитным
сердечником. Используя приведенные
выше формулы для коэффициента самоиндукции
L_μ
соленоида и для магнитного поля B,
создаваемого током I,
можно получить:

где
V– объем соленоида. Это выражение
показывает, что магнитная энергия
локализована не в витках катушки, по
которым протекает ток, а рассредоточена
по всему объему, в котором создано
магнитное поле. Физическая величина

равная
энергии магнитного поля в единице
объема, называется объемной
плотностью магнитной энергии.
Дж. Максвелл
показал, что выражение для объемной
плотности магнитной энергии, выведенное
здесь для случая длинного соленоида,
справедливо для любых магнитных полей.

Теоретическое обоснование

Электрическая цепь постоянного тока и ее характеристики

Если в проводящем контуре течёт ток, то ток создаёт магнитное поле.

Будем вести рассмотрение в квазистатическом приближении, подразумевая, что переменные электрические поля достаточно слабы либо меняются достаточно медленно, чтобы можно было пренебречь порождаемыми ими магнитными полями.

Ток считаем одинаковым по всей длине контура (пренебрегая ёмкостью проводника, которая позволяет накапливать заряды в разных его участках, что вызвало бы неодинаковость тока вдоль проводника и заметно усложнило бы картину).

По закону Био — Савара — Лапласа, величина вектора магнитной индукции, создаваемой некоторым элементарным (в смысле геометрической малости участка проводника, рассматриваемого как элементарный источник магнитного поля) током в каждой точке пространства, пропорциональна этому току. Суммируя поля, создаваемые каждым элементарным участком, приходим к тому, что и магнитное поле (вектор магнитной индукции), создаваемое всем проводником, также пропорционально порождающему току.

Рассуждение выше верно для вакуума. В случае присутствия магнитной среды (магнетика) с заметной (или даже большой) магнитной восприимчивостью, вектор магнитной индукции (который и входит в выражение для магнитного потока) будет заметно (или даже во много раз) отличаться от того, каким бы он был в отсутствие магнетика (в вакууме). Мы ограничимся здесь линейным приближением, тогда вектор магнитной индукции, хотя, возможно, возросший (или уменьшившийся) в заметное количество раз по сравнению с отсутствием магнетика при том же контуре с током, тем не менее остаётся пропорциональным порождающему его току.

Тогда магнитный поток, то есть поток поля вектора магнитной индукции:

Φ=∫SB⋅dS{\displaystyle \Phi =\int \limits _{S}\mathbf {B} \cdot \mathbf {dS} }

через любую конкретную фиксированную поверхность S (в частности и через интересующую нас поверхность, краем которой является наш контур с током) будет пропорционален току, так как пропорционально току B всюду под интегралом.

Заметим, что поверхность, краем которой является контур, может быть достаточно сложна, если сложен сам контур. Уже для контура в виде просто многовитковой катушки такая поверхность оказывается достаточно сложной. На практике это приводит к использованию некоторых упрощающих представлений, позволяющих легче представить такую поверхность и приближённо рассчитать поток через неё (а также в связи с этим вводятся некоторые дополнительные специальные понятия, подробно описанные в отдельном параграфе ниже). Однако здесь, при чисто теоретическом рассмотрении нет необходимости во введении каких-то дополнительных упрощающих представлений, достаточно просто заметить, что как бы ни был сложен контур, в данном параграфе мы имеем в виду «полный поток» — то есть поток через всю сложную (как бы многолистковую) поверхность, натянутую на все витки катушки (если речь идет о катушке), то есть о том, что называется потокосцеплением. Но поскольку нам здесь не надо конкретно рассчитывать его, а нужно только знать, что он пропорционален току, нам не слишком интересен конкретный вид поверхности, поток через которую нас интересует (ведь свойство пропорциональности току сохраняется для любой).

Итак, мы обосновали:

Φ {\displaystyle \Phi \ }~ I,{\displaystyle \ I,}

этого достаточно, чтобы утверждать, введя обозначение L для коэффициента пропорциональности, что

Φ=LI.{\displaystyle \Phi =LI.}

В заключение теоретического обоснования покажем, что рассуждение корректно в том смысле, что магнитный поток не зависит от конкретной формы поверхности, натянутой на контур. (Действительно, даже на самый простой контур может быть натянута — в том смысле, что контур должен быть её краем — не единственная поверхность, а разные, например, начав с двух совпадающих поверхностей, затем одну поверхность можно немного прогнуть, и она перестанет совпадать со второй). Поэтому надо показать, что магнитный поток одинаков для любых поверхностей, натянутых на один и тот же контур.

Но это действительно так: возьмём две такие поверхности. Вместе они будут составлять одну замкнутую поверхность. А мы знаем (из закона Гаусса для магнитного поля), что магнитный поток через любую замкнутую поверхность равен нулю. Это (с учетом знаков) означает, что поток через одну поверхность и другую поверхность — равны. Что доказывает корректность определения.

Ресчет катушек индуктивности однослойных, цилиндрических

Катушка Тесла на одном транзисторе или качер Бровина

Рис. 1. Пример однослойной катушки индуктивности.

Все приведенные выше соображения справедливы при намотке катушек без ферритовых сердечников. Расчет однослойных цилиндрических катушек производится по формуле:

где:

L — индуктивность катушки, мкГн;
D — диаметр катушки, см;
I — длина намотки катушки, см;
n — число витков катушки.

При расчете катушки могут встретиться два случая:

а) по заданным геометрическим размерам необходимо определить индуктивность катушки;
б) при известной индуктивности определить число витков и диаметр провода катушки.

В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.

Пример. Определим индуктивность катушки, изображенной на рис. 1; для этого подставим в формулу все необходимые величины:

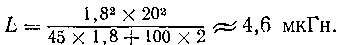
Во втором случае известны диаметр катушки и длина намотки, которая, в свою очередь, зависит от числа витков и диаметра провода.

Поэтому расчет рекомендуется вести в следующей последовательности. Исходя из конструктивных соображений определяют размеры катушки, диаметр и длину намотки, а затем рассчитывают число витков по формуле:

После того как будет найдено число витков, определяют диаметр провода с изоляцией по формуле:

где:

d — диаметр провода, мм,
l — длина обмотки, мм,
n — число витков.

Пример. Нужно изготовить катушку диаметром 1 см при длине намотки 2 см, имеющую индуктивность 0,8 мкГн. Намотка рядовая виток к витку.

Подставив в последнюю формулу заданные величины, получим:

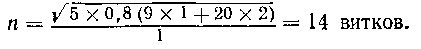
Диаметр провода:

Если эту катушку наматывать проводом меньшего диаметра, то нужио полученные расчетным путем 14 витков разместить по всей длине катушки (20 мм) с равными промежутками между витками, т. е. с шагом намотки.

Индуктивность данной катушки будет на 1—2% меньше номинальной, что следует учитывать при изготовлении таких катушек. При намотке в случае необходимости более толстым проводом, чем 1,43 мм, следует сделать новый расчет, увеличив диаметр или длину намотки катушки.

Возможно, также придется увеличить и то и другое одновременно, пока не будут получепы необходимые габариты катушки, соответствующие заданной индуктивности.

Следует заметить, что по приведенным пыше формулам рекомендуется рассчитывать такие катушки, у которых длина намотки l равна или больше половины диаметра. Если же длина намотки меньше D половины диаметра то более точные результаты можно получить по формулам:

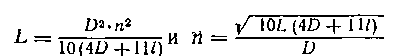
Методы расчета индуктивностей

Применение трансформаторов напряжения

Наиболее полно теоретические основы методов расчета индуктивностей изложены в справочной книге: «». Здесь же хотелось бы немного систематизировать подходы к расчету индуктивностей.

Прежде всего отметим, что расчет индуктивности можно вести двумя способами:∙ Численный метод с различной степенью упрощения задачи ∙ Расчет по упрощенным эмпирическим формулам

Эмпирический подход предполагает подбор (подгонку) относительно несложных аппроксимирующих формул по результатам измерений индуктивности реальных катушек. Расчет по упрощенным эмпирическим формулам имеет ограничения в точности и применим только к катушкам с определенной геометрией намотки. Большинство таких формул можно найти здесь. Несмотря на невысокую точность, такой расчет чаще всего вполне достаточен в радиолюбительской практике.

Численные методы основываются на реальных физических моделях катушек индуктивности и их, в свою очередь, можно разбить на две категории:

Расчет в программах основанных на фундаментальных законах классической электродинамики, так называемых электромагнитных симуляторах. К ним можно отнести , , , и т.п. Эти программы используют специальные численные методы, такие как и . Расчет в таких программах довольно точен, позволяет учесть множество нюансов, рассчитать катушку произвольной формы, однако требует огромных ресурсов компьютера. Применяется при научном анализе или если катушка работает в режиме, когда ее нельзя представлять как сосредоточенный элемент []
Численные методы расчета, основанные на фундаментальных формулах физики, применимых к круговым проводникам, выведенных в XIX веке . Позволяют провести расчет более точно, чем по эмпирическим формулам, но не требуют запредельных аппаратных ресурсов компьютера. На них следует остановится подробнее, т.к их и использует Coil32…

Расчет индуктивности в программе Coil32 основан на модели Максвелла, в которой катушка представляется как множество соосных бесконечно тонких круговых проводников.Из следует, что силовые линии магнитного поля всегда замкнуты. Из этого следует, что магнитный поток порожденный круговым контуром с током весь проходит через поверхность, ограниченную этим контуром. Это обстоятельство отражено в следующей формуле:

Из этой формулы можно вывести определение для собственной индуктивности кругового проводника через двойной контурный интеграл Ф.Е.Неймана для взаимоиндукции :

Как показал Д.К.Максвелл, для двух бесконечно тонких круговых соосных проводников этот интеграл имеет однозначное решение, которое выглядит следующим образом:

, где:

M — взаимоиндукция;
r₁, r₂ — радиусы двух бесконечно тонких круговых проводников;
x — расстояние между центрами кругов, ограниченных этими проводниками;
K,E — , соответственно первого и второго рода;

Численный метод расчета по формуле Максвелла сводится к численным методам решения эллиптических интегралов.

По формуле Максвелла можно рассчитывать как индуктивность многослойных и однослойных катушек, так и взаимную индуктивность двух отдельных катушек. Погрешности модели, связанные с допущением, что провод бесконечно тонкий и представляет собой набор круговых проводников (хотя на самом деле — это спираль), можно уменьшить с помощью соответствующих поправок.

Рассчитывая взаимоиндукцию проводника «самого на себя», т.е. его самоиндукцию (собственную индуктивность), Максвелл использует понятие — «среднее геометрическое расстояние» — GDM (g), для круглого провода:

g = e0.25*r_w, где r_w — радиус провода.

Очень важен следующий момент. Вся вышеприведенная логика рассуждений и вывода формул, начиная от формулы Неймана, справедлива в случае равномерного распределения плотности тока вдоль катушки. В подавляющем большинстве практических случаев так и есть. Однако если катушка работает вблизи частот собственного резонанса, начинает проявляться неравномерность распределения плотности тока по проводнику! Другими словами, начинает проявляться зависимость индуктивности от частоты, которая в наших расчетах не учитывается. Поэтому индуктивность катушки можно рассчитать корректно только на частотах не превышающих 60-70% от частоты ее собственного резонанса. Таким образом Coil32 не годится для точных расчетов, например, катушек Тесла или спиральных резонаторов. В этом случае и в случае если катушка работает в режиме выше частоты собственного резонанса — ее нужно представлять только в виде модели длинной линии и рассчитывать в программах-электромагнитных симуляторах, либо пользоваться специальными эмпирическими формулами.

Ссылки:

D W Knight 2013
Robert Weaver 2012
Marc T. Thompson 1999
M.A.Bueno A K T Assis 1995

Индуктивность длинного прямого проводника

Для длинного прямого (или квазилинейного) провода кругового сечения индуктивность выражается приближённой формулой:

L=μ2πl(μelnlr+14μi),{\displaystyle L={\frac {\mu _{0}}{2\pi }}l{\Big (}\mu _{e}\mathrm {ln} {\frac {l}{r}}+{\frac {1}{4}}\mu _{i}{\Big )},}

где μ{\displaystyle \mu _{0}} − магнитная постоянная, μe{\displaystyle \mu _{e}} — относительная магнитная проницаемость внешней среды (которой заполнено пространство (для вакуума μe=1{\displaystyle \mu _{e}=1}), μi{\displaystyle \mu _{i}} — относительная магнитная проницаемость материала проводника, l{\displaystyle l} — длина провода, rl{\displaystyle r
— радиус его сечения.

Физика для средней школы

Индуктивность. Явление самоиндукции

Электрический ток, проходящий по контуру, создает вокруг него магнитное поле. Магнитный поток Ф через контур этого проводника (его называют собственным магнитным потоком) пропорционален модулю индукции В магнитного поля внутри контура, а индукция магнитного поля в свою очередь пропорциональна силе тока в контуре.

Следовательно, собственный магнитный поток через контур прямо пропорционален силе тока в контуре:

Коэффициент пропорциональности L между силой тока I в контуре и магнитным потоком Ф, создаваемым этим током, называется индуктивностью контура. Индуктивность контура зависит от размеров и формы контура, от магнитных свойств среды, в которой находится контур. Так, индуктивность однослойного соленоида можно рассчитать по формуле

где — магнитная проницаемость сердечника, — магнитная постоянная, N — число витков соленоида, S — площадь витка, l — длина соленоида.

Единицей индуктивности в СИ является генри (Гн). Эта единица определяется на основании формулы

Индуктивность контура равна 1 Гн, если при силе постоянного тока 1 А магнитный поток через контур равен 1 Вб: 1 Гн = (1 Вб)А

Если в контуре проходит постоянный ток то вокруг контура существует постоянное
магнитное поле. Собственный магнитный поток пронизывающий контур неизменяется стечением времени и ЭДС индукции в этом контуре невозбуждается. Если же ток проходящий в контуре будет изменяться со временем то, соответственно изменяющийся собственный магнитный поток, согласно закону электромагнитной индукции создает в контуре ЭДС. Возникновение ЭДС индукции в контуре которое вызвано изменением магнитного поля тока проходящего в этом же контуре называют явлением самоиндукции, а появляющуюся ЭДС — ЭДС самоиндукции. ЭДС самоиндукции создает в контуре ток самоиндукции.

Направление тока самоиндукции определяется по правилу Ленца: ток самоиндукции всегда направлен так, что он противодействует изменению основного тока. Если основной ток возрастает, то ток самоиндукции направлен против основного тока, если уменьшается, то направления основного тока и тока самоиндукции совпадают.

По закону электромагнитной индукции среднее значение ЭДС самоиндукции, возникающей в контуре с индуктивностью L (индуктивность контура не изменяется),

Мгновенное значение ЭДС

ЭДС самоиндукции прямо пропорциональна индуктивности контура и скорости изменения силы тока в контуре.

Из этой формулы следует, что индуктивность — физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

Используя это выражение, можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 А за 1 с в нем возникает ЭДС самоиндукции 1 В.

Изменить магнитный поток можно также путем изменения индуктивности контура.

В общем случае может изменяться как сила тока в контуре, так и его индуктивность. Тогда среднее значение ЭДС самоиндукции

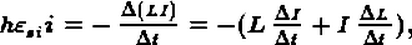
a ее мгновенное значение

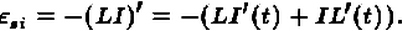
Примерами самоиндукции являются экстратоки замыкания и размыкания.

Собирают электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока (рис. 1). Резистор должен иметь такое же электрическое сопротивление, как и катушка. Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором.

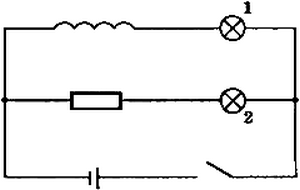
Рис. 1

Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке. При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке. На рисунке 2 изображены графики изменения тока через лампочку 1 при замыкании (а) и размыкании (б) цепи. Явление самоиндукции создает искру в том месте, где происходит размыкание цепи. Если в цепи имеются мощные электромагниты, то искра может перейти в дуговой разряд и испортить выключатель.

Для размыкания таких цепей на электростанциях пользуются масляными выключателями. В линиях электропередачи предусматриваются специальные автоматические выключатели, размещенные в отдельных зданиях и снабженные искрогасительными устройствами.

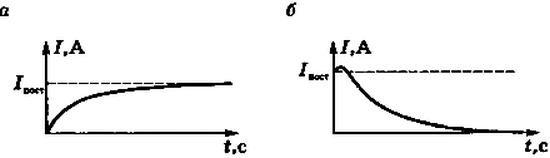
Рис. 2

Индуктивность тороидальной катушки катушки с кольцевым сердечником

Тороидальная катушка

Для тороидальной катушки, намотанной на сердечнике из материала с большой магнитной проницаемостью, можно приближённо пользоваться формулой для бесконечного прямого соленоида ():

L=N2⋅μμS2πr,{\displaystyle L=N^{2}\cdot {\frac {\mu _{0}\mu S}{2\pi r}},\,}

где 2πr{\displaystyle 2\pi r} — оценка длины соленоида (r{\displaystyle r} — средний радиус тора).
Лучшее приближение дает формула

L=N2⋅μμh2π⋅ln⁡Rr,{\displaystyle L=N^{2}\cdot {\frac {\mu _{0}\mu h}{2\pi }}\cdot \ln {\frac {R}{r}},\,}

где предполагается сердечник прямоугольного сечения с наружным радиусом R и внутренним радиусом r, высотой h.

Разновидности катушек индуктивности

Контурные катушки индуктивности, используемые в радиотехнике: Эти катушки используются совместно с конденсаторами для организации резонансных контуров. Они должны иметь высокую термо- и долговременную стабильность, и добротность, требования к паразитной ёмкости обычно несущественны.

Катушки связи, или трансформаторы связи: Взаимодействующие магнитными полями пара и более катушек обычно включаются параллельно конденсаторам для организации колебательных контуров. Такие катушки применяются для обеспечения трансформаторной связи между отдельными цепями и каскадами, что позволяет разделить по постоянному току, например, цепь базы последующего усилительного каскада от коллектора предыдущего каскада и т. д. К нерезонансным разделительным трансформаторам не предъявляются жёсткие требования на добротность и точность, поэтому они выполняются из тонкого провода в виде двух обмоток небольших габаритов. Основными параметрами этих катушек являются индуктивность и коэффициент связи (коэффициент взаимоиндукции).

Вариометры: Это катушки, индуктивностью которых можно управлять (например, для перестройки частоты резонанса колебательных контуров) изменением взаимного расположения двух катушек, соединённых последовательно. Одна из катушек неподвижная (статор), другая обычно располагается внутри первой и вращается (ротор). Существуют и другие конструкции вариометров. При изменении положения ротора относительно статора изменяется степень взаимоиндукции, а следовательно, индуктивность вариометра. Такая система позволяет изменять индуктивность в 4 − 5 раз. В ферровариометрах индуктивность изменяется перемещением ферромагнитного сердечника относительно обмотки, либо изменением длины воздушного зазора замкнутого магнитопровода.

Дроссели: Это катушки индуктивности, обладающие высоким сопротивлением переменному току и малым сопротивлением постоянному. Дроссели включаются последовательно с нагрузкой для ограничения переменного тока в цепи, они часто применяются в цепях питания радиотехнических устройств в качестве фильтрующего элемента, а также в качестве балласта для включения разрядных ламп в сеть переменного напряжения. Для сетей питания с частотами 50-60 Гц выполняются на сердечниках из трансформаторной стали. На более высоких частотах также применяются сердечники из пермаллоя или феррита. Особая разновидность дросселей — помехоподавляющие ферритовые бочонки (бусины или кольца), нанизанные на отдельные провода или группы проводов (кабели) для подавления синфазных высокочастотных помех.

Сдвоенный дроссель

Сдвоенные дроссели: Это две намотанных встречно или согласованно катушки индуктивности, используются в фильтрах питания. За счёт встречной намотки и взаимной индукции более эффективны для фильтрации синфазных помех при тех же габаритах. При согласной намотке эффективны для подавления дифференциальных помех. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания; в дифференциальных сигнальных фильтрах цифровых линий, а также в звуковой технике.Предназначены как для защиты источников питания от попадания в них наведённых высокочастотных сигналов из питающей сети, так и во избежание проникновения в питающую сеть электромагнитных помех, генерируемых устройством. На низких частотах используется в фильтрах цепей питания и обычно имеет ферромагнитный сердечник (из трансформаторной стали). Для фильтрации высокочастотных помех — сердечник ферритовый.

Применение катушек индуктивности

Балластный дроссель. Конструкция, применяющаяся в качестве реактивного сопротивления для разрядных ламп на частоте 50 — 60 Гц. В связи с заметной зависимостью сопротивления дросселя от режима работы и от частотного спектра тока сопротивление дросселя определяется как отношение напряжения к току при замкнутой лампе и токе через дроссель, равный рабочему току лампы. В электронном пуско-регулирующем аппарате для люминесцентной лампы, работающем на частоте 20 — 50 кГц, дроссель изготавливается на ферритовом сердечнике и имеет существенно меньшие размеры.

Катушки индуктивности (совместно с конденсаторами и/или резисторами) используются для построения различных цепей с частотно-зависимыми свойствами, в частности, фильтров, цепей обратной связи, колебательных контуров и т. п.
Катушки индуктивности используются в импульсных стабилизаторах как элемент, накапливающий энергию и преобразующий уровни напряжения.
Две и более индуктивно связанные катушки образуют трансформатор.
Катушка индуктивности, питаемая импульсным током от транзисторного ключа, иногда применяется в качестве источника высокого напряжения небольшой мощности в слаботочных схемах, когда создание отдельного высокого питающего напряжения в блоке питания невозможно или экономически нецелесообразно. В этом случае на катушке из-за самоиндукции возникают выбросы высокого напряжения, которые можно использовать в схеме, например, выпрямив и сгладив.
Катушки используются также в качестве электромагнитов — исполнительных механизмов.
Катушки применяются в качестве источника энергии для нагрева индуктивно-связанной плазмы, а также её диагностики.
Для радиосвязи — приёма электромагнитных волн, редко — для излучения:
- Ферритовая антенна
- Рамочная антенна, кольцевая антенна
- DDRR
- Индукционная петля
Для разогрева электропроводящих материалов в индукционных печах.
Как датчик перемещения: изменение индуктивности катушки может изменяться в широких пределах при перемещении ферромагнитного сердечника относительно обмотки.
Катушка индуктивности используется в индукционных датчиках магнитного поля в индукционных магнитометрах
Для создания магнитных полей в ускорителях элементарных частиц, магнитного удержания плазмы, в научных экспериментах, в ядерно-магнитной томографии. Мощные стационарные магнитные поля, как правило, создаются сверхпроводящими катушками.
Для накопления энергии.

Таблица индуктивностей

Символ μ{\displaystyle \mu _{0}} обозначает магнитную постоянную (4π⋅10−7 Гн/м). В высокочастотном случае ток течёт в поверхности проводников (скин-эффект) и в зависимости от вида проводников иногда нужно различать индуктивность высокой и низкои частоты. Для этого служит постоянная Y: Y = 0, когда ток равномерно распределён по поверхности провода (скин-эффект), Y = 1⁄₄, когда ток равномерно распределён по поперечному сечению провода. В случае скин-эффекта нужно учитывать, что при маленьких расстояниях между проводниками в поверхностях текут дополнительные вихревые токи (эффект экранирования), и выражения, содержащие Y, становятся неточными.

Коэффициенты самоиндукции некоторых замкнутых контуров
Вид	Индуктивность	Комментарий
соленоидс тонкой обмоткой	μr2N23l−8w+41+mm(K(m1+m)−(1−m)E(m1+m)){\displaystyle {\frac {\mu _{0}r^{2}N^{2}}{3l}}\left} =μr2N2πl1−8w3π+∑n=1∞(2n)!2n!4(n+1)(2n−1)22n(−1)n+1w2n{\displaystyle ={\frac {\mu _{0}r^{2}N^{2}\pi }{l}}\left}=μr2N2πl(1−8w3π+w22−w44+5w616−35w864+…){\displaystyle ={\frac {\mu _{0}r^{2}N^{2}\pi }{l}}\left(1-{\frac {8w}{3\pi }}+{\frac {w^{2}}{2}}-{\frac {w^{4}}{4}}+{\frac {5w^{6}}{16}}-{\frac {35w^{8}}{64}}+…\right)} для w =μrN2(1+132w2+O(1w4))ln⁡(8w)−12+1128w2+O(1w4){\displaystyle =\mu _{0}rN^{2}\left[\left(1+{\frac {1}{32w^{2}}}+O\left({\frac {1}{w^{4}}}\right)\right)\ln(8w)-1/2+{\frac {1}{128w^{2}}}+O\left({\frac {1}{w^{4}}}\right)\right]} для w >> 1	N: Число витковr: Радиусl: Длинаw = r/lm = 4w2E,K: Эллиптический интеграл
Коаксиальный кабель,высокая частота	μl2πln⁡(a1a){\displaystyle {\frac {\mu _{0}l}{2\pi }}\ln \left({\frac {a_{1}}{a}}\right)}	a₁: Радиусa: Радиусl: Длина
единичныйкруглый виток	μr⋅(ln⁡(8ra)−2+Y+O(a2r2)){\displaystyle \mu _{0}r\cdot \left(\ln \left({\frac {8r}{a}}\right)-2+Y+O\left(a^{2}/r^{2}\right)\right)}	r: Радиус виткаa: Радиус проволоки
прямоугольник	μπ(bln⁡(2ba)+dln⁡(2da)−(b+d)(2−Y)+2b2+d2){\displaystyle {\frac {\mu _{0}}{\pi }}\left(b\ln \left({\frac {2b}{a}}\right)+d\ln \left({\frac {2d}{a}}\right)-\left(b+d\right)\left(2-Y\right)+2{\sqrt {b^{2}+d^{2}}}\right)} −μπ(b⋅arsinh⁡(bd)+d⋅arsinh⁡(db)+O(a)){\displaystyle \;\;-{\frac {\mu _{0}}{\pi }}\left(b\cdot \operatorname {arsinh} \left({\frac {b}{d}}\right)+d\cdot \operatorname {arsinh} \left({\frac {d}{b}}\right)+O\left(a\right)\right)}	b, d: Длины краёвd >> a, b >> aa: Радиус проволоки
Две параллельныепроволоки	μlπ(ln⁡(da)+Y){\displaystyle {\frac {\mu _{0}l}{\pi }}\left(\ln \left({\frac {d}{a}}\right)+Y\right)}	a: Радиус проволокиd: Расстояние, d ≥ 2al: Длина пары
Две параллельныепроволоки, высокаячастота	μlπarcosh⁡(d2a)=μlπln⁡(d2a+d24a2−1){\displaystyle {\frac {\mu _{0}l}{\pi }}\operatorname {arcosh} \left({\frac {d}{2a}}\right)={\frac {\mu _{0}l}{\pi }}\ln \left({\frac {d}{2a}}+{\sqrt {{\frac {d^{2}}{4a^{2}}}-1}}\right)}	a: Радиус проволокиd: Расстояние, d ≥ 2al: Длина пары
Проволока параллельнаидеально проводящейстене	μl2π(ln⁡(2da)+Y){\displaystyle {\frac {\mu _{0}l}{2\pi }}\left(\ln \left({\frac {2d}{a}}\right)+Y\right)}	a: Радиус проволокиd: Расстояние, d ≥ al: Длина
Проволока параллельнастене,высокая частота	μl2πarcosh⁡(da)=μl2πln⁡(da+d2a2−1){\displaystyle {\frac {\mu _{0}l}{2\pi }}\operatorname {arcosh} \left({\frac {d}{a}}\right)={\frac {\mu _{0}l}{2\pi }}\ln \left({\frac {d}{a}}+{\sqrt {{\frac {d^{2}}{a^{2}}}-1}}\right)}	a: Радиус проволокиd: Расстояние, d ≥ al: Длина

Применение в технике

Катушки индуктивности применяются:

Рис. 9. Катушки индуктивности

Для подавления помех, сглаживания пульсаций, накопления энергии, ограничения переменного тока, в резонансных (колебательный контур) и частотно-избирательных цепях; создания магнитных полей, датчиков перемещений, в считывающих устройствах кредитных карт, а также в самих бесконтактных кредитных картах.
Катушки индуктивности (совместно с конденсаторами и резисторами) используются для построения различных цепей с частотно-зависимыми свойствами, в частности, фильтров, цепей обратной связи, колебательных контуров и других. Такие катушки, соответственно, так и называют: контурная катушка, катушка фильтра и так далее.
Две индуктивно связанные катушки образуют трансформатор.
Катушка индуктивности, питаемая импульсным током от транзисторного ключа, иногда применяется в качестве источника высокого напряжения небольшой мощности в слаботочных схемах, когда создание отдельного высокого питающего напряжения в блоке питания невозможно или экономически нецелесообразно. В этом случае на катушке из-за самоиндукции возникают выбросы высокого напряжения, которые можно использовать в схеме.
При использовании для подавления помех, сглаживания пульсаций электрического тока, изоляции (развязки) по высокой частоте разных частей схемы и накопления энергии в магнитном поле сердечника катушку индуктивности называют дросселем.
В силовой электротехнике (для ограничения тока при, например, коротком замыкании ЛЭП) катушку индуктивности называют реактором.
Ограничители тока сварочных аппаратов выполняются в виде катушки индуктивности, ограничивая ток сварочной дуги и делая её более стабильной, тем самым позволяя получить более ровный и прочный сварочный шов.
Катушки индуктивности используются также в качестве электромагнитов — исполнительных механизмов. Цилиндрическую катушку индуктивности, длина которой намного превышает диаметр, называют соленоидом. Кроме того, зачастую соленоидом называют устройство, выполняющее механическую работу за счёт магнитного поля при втягивании ферромагнитного сердечника.
В электромагнитных реле катушки индуктивности называют обмоткой реле.
Нагревательный индуктор — специальная катушка индуктивности, рабочий орган установок индукционного нагрева и кухонных индукционных печей.

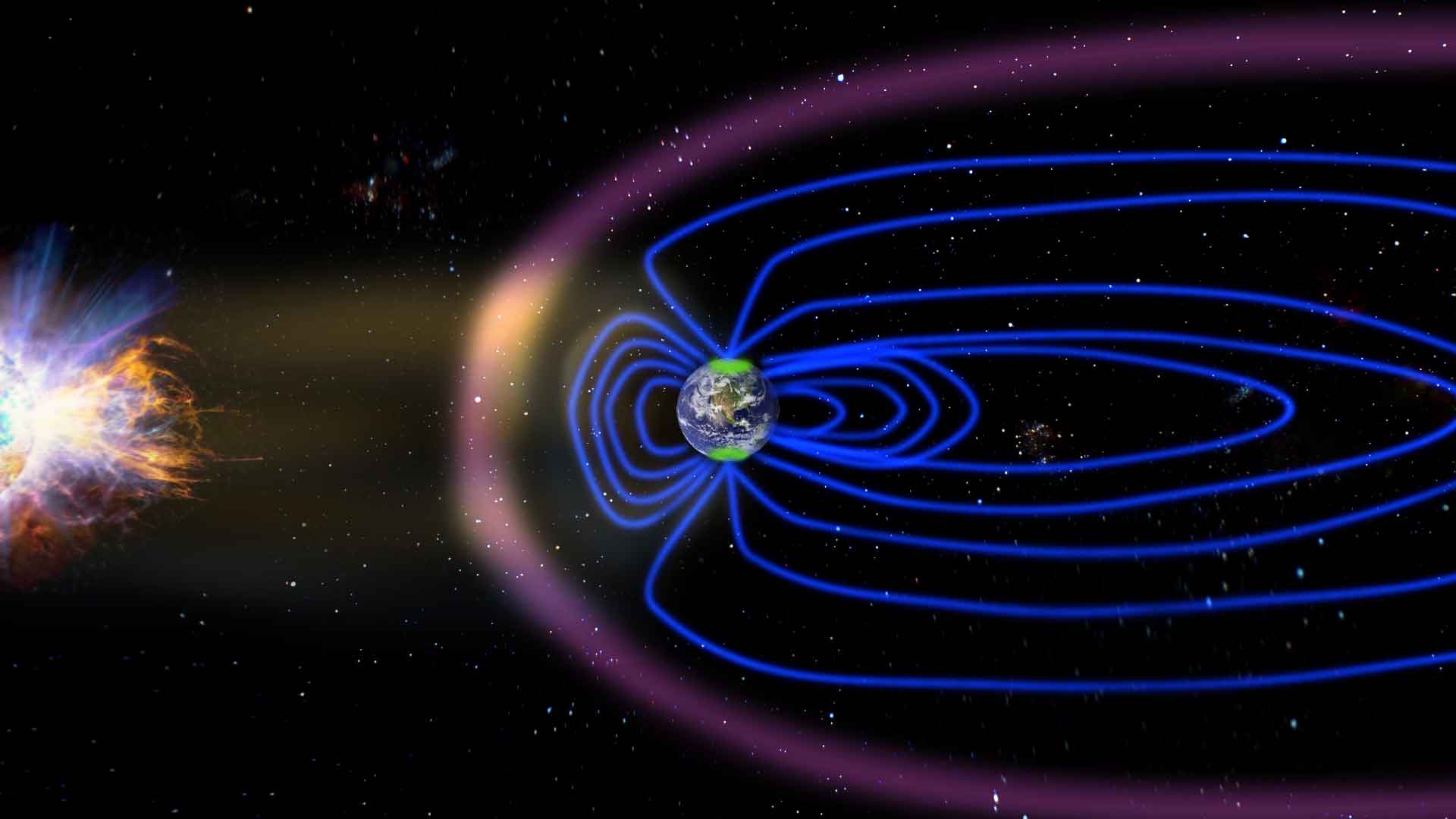
По большому счёту, во всех генераторах электрического тока любого типа, равно как и в электродвигателях, их обмотки представляют собой катушки индуктивности. Следуя традиции древних изображения плоской Земли, стоящей на трёх слонах или китах, сегодня мы могли бы с большим основанием утверждать, что жизнь на Земле покоится на катушке индуктивности.

Рис. 15. Магнитосфера Земли

Ведь даже магнитное поле Земли, защищающее все земные организмы от корпускулярного космического и солнечного излучений, согласно основной гипотезе о его происхождении, связано с протеканием огромных токов в жидком металлическом ядре Земли. По сути дела, это ядро представляет собой катушку индуктивности планетарного масштаба. Подсчитано, что зона, в которой действует механизм «магнитного динамо», находится на расстоянии 0,25—0,3 радиуса Земли.

Рис. 7. Магнитное поле вокруг проводника с током. I — ток, B — вектор магнитной индукции.