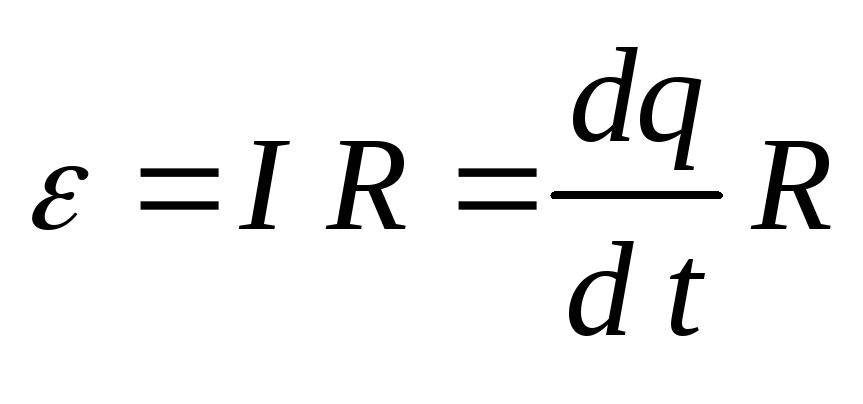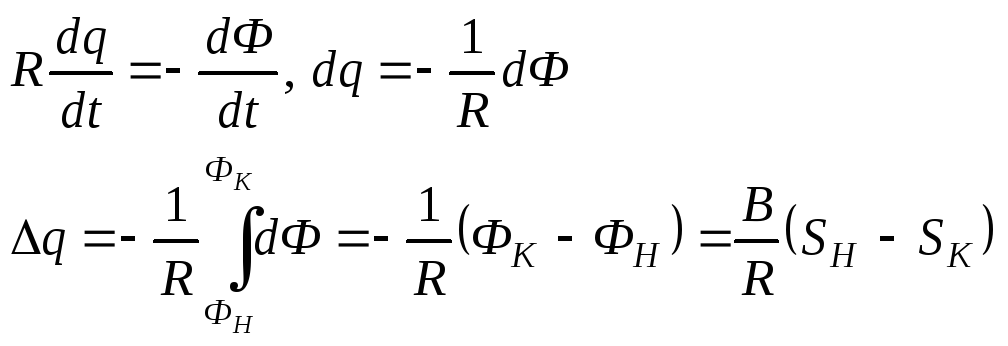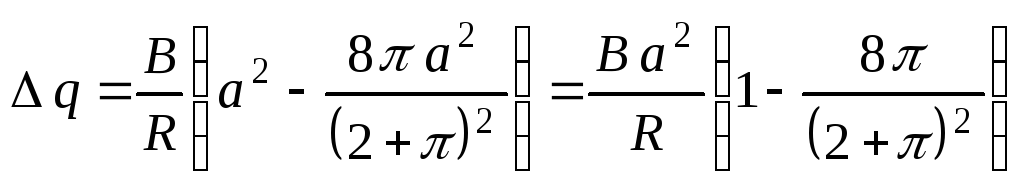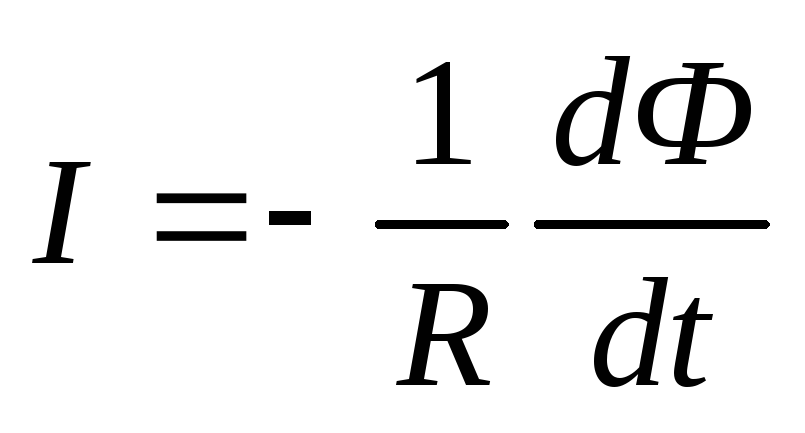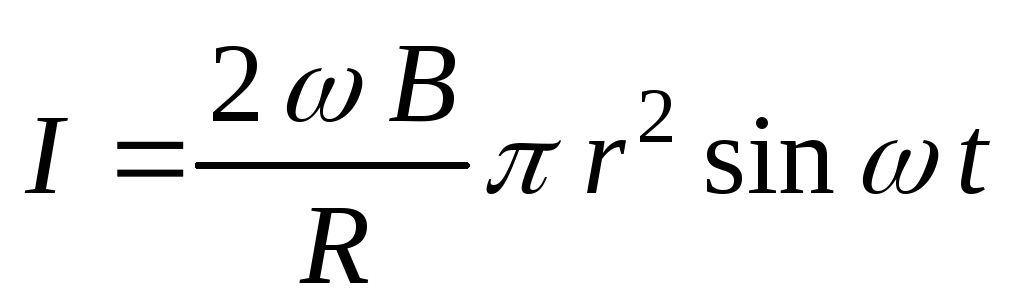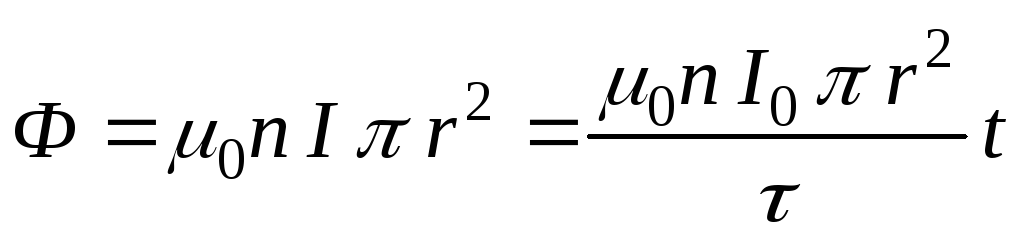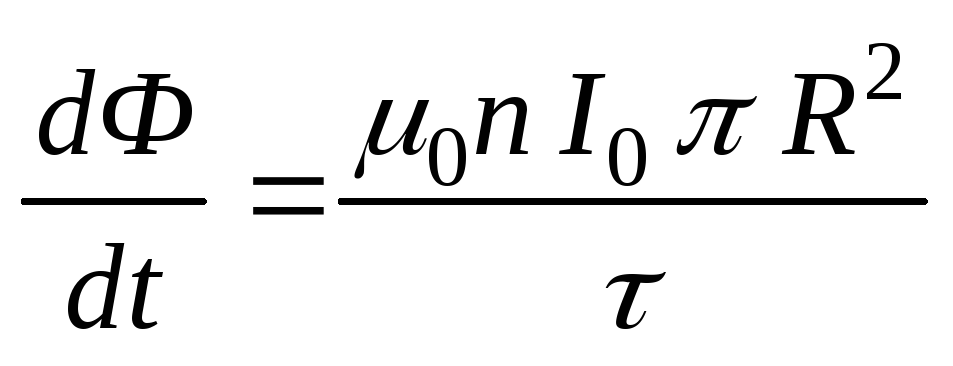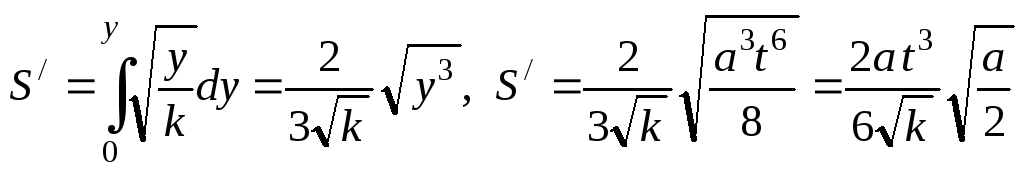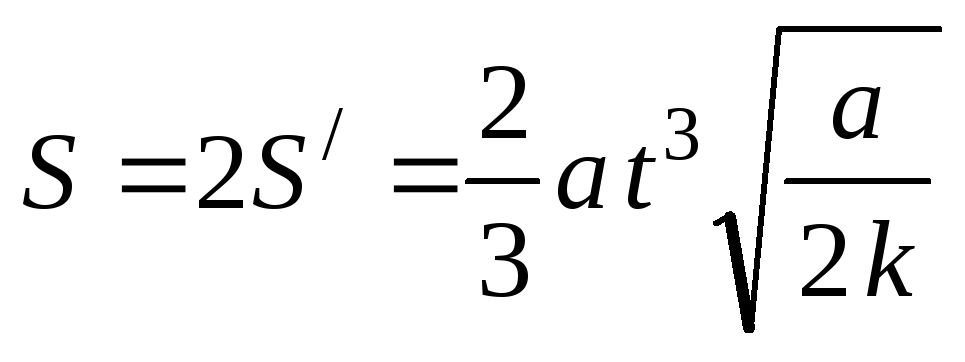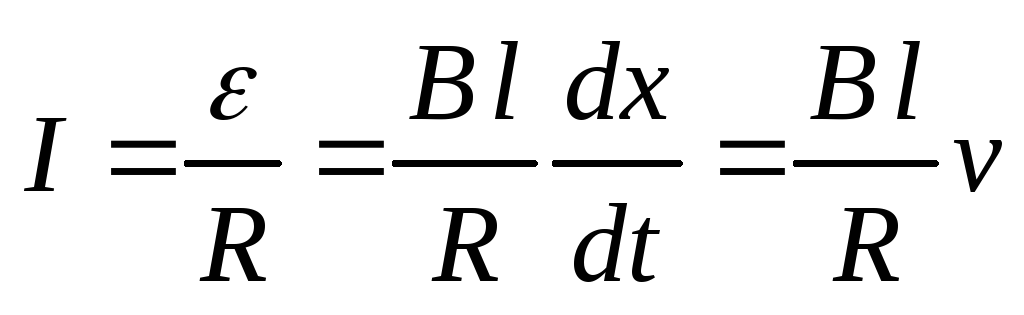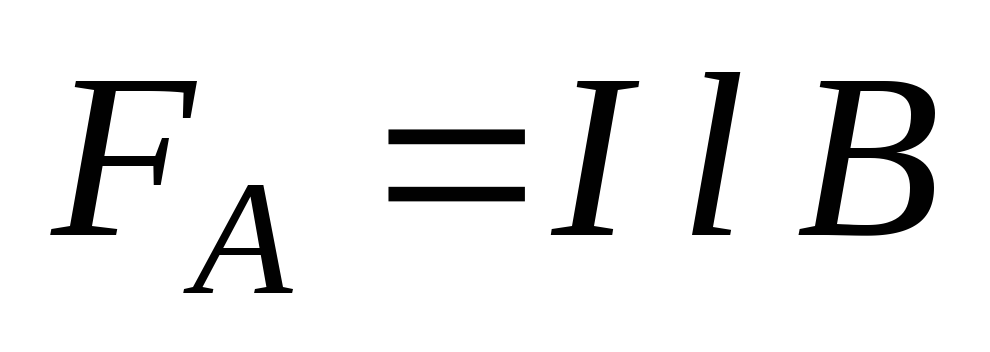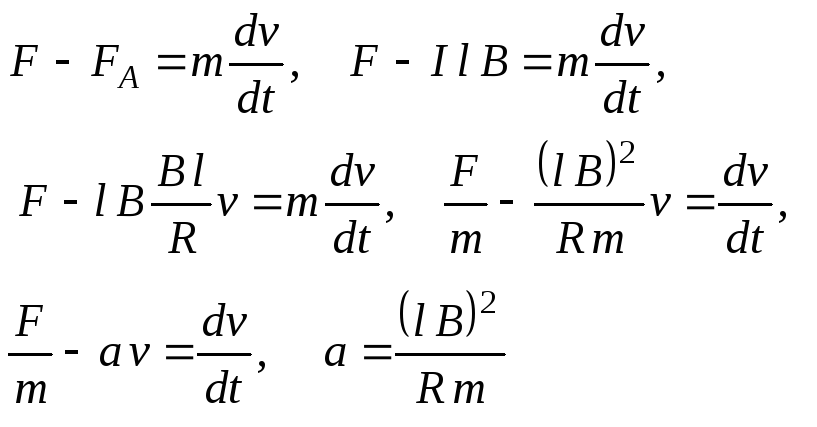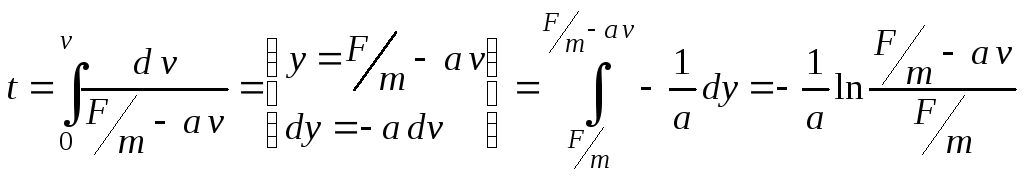Закон ЭДС индукции Фарадея для трансформаторов

Исследования электромагнетизма

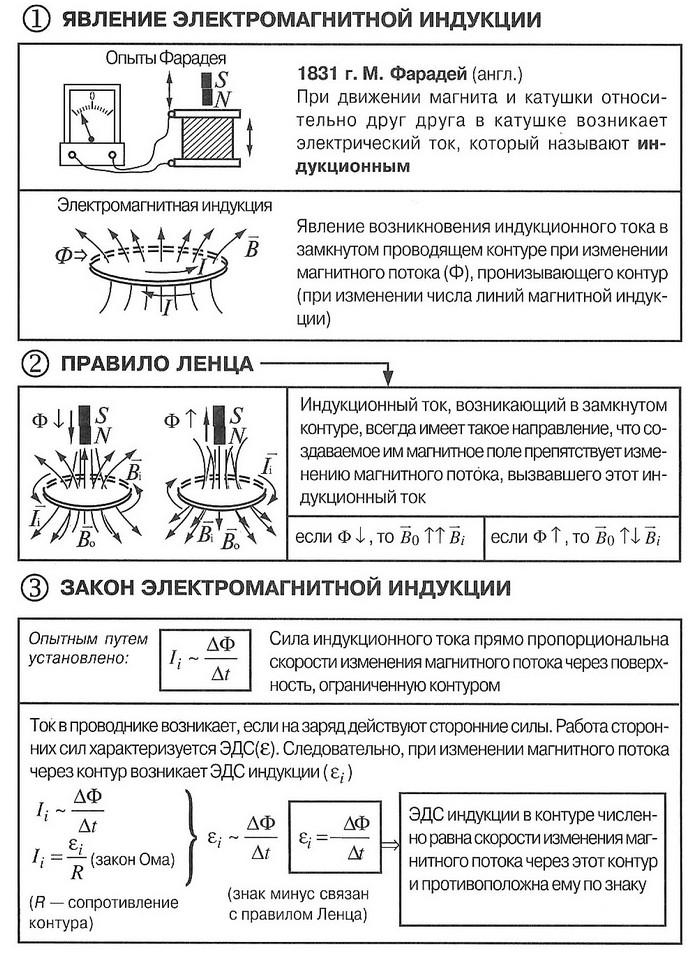
Явление электромагнитной индукции заключается в наведении ЭДС в проводнике под действием изменяющегося магнитного поля. Сегодня на этом принципе работают приборы, начиная трансформаторами и заканчивая варочными панелями. Первенство в области отдано Гансу Эрстеду, 21 апреля 1820 года заметившему действие замкнутой цепи на стрелку компаса. Подобные наблюдения публиковались в виде заметок Джованни Доменико Романьози в 1802 году.

Джованни Доменико Романьози

Заслуга датского учёного в привлечении к делу многих видных учёных. Итак, замечено, что стрелка отклоняется проводником с током, и осенью упомянутого года появился на свет первый гальванометр. Измерительный прибор на ниве электричества стал большим подспорьем многим. Попутно высказывались различные точки зрения, в частности, Волластон огласил, что неплохо заставить проводник с током вращаться непрерывно под действием магнита. В 20-е годы XIX века вокруг указанного вопроса царила эйфория, до этого магнетизм и электричество считались независимыми явлениями.

Оенью 1821 года задумку воплотил в жизнь Майкл Фарадей. Утверждают, что тогда на свет появился первый электрический двигатель. 12 сентября 1821 года в письме Гаспару де ла Риву Фарадей пишет:

«Я выяснил, что притяжения и отталкивания магнитной стрелки проводом с током — детская забава. Некая сила станет вращать непрерывно магнит под действием электрического тока. Я построил теоретические выкладки и сумел реализовать на практике».

Письмо к де ла Риву не стало случайностью. По мере становления на научном поприще Фарадей обрёл немало сторонников и единственного непримиримого противника… сэра Хампфри Дэви. Экспериментальная установка объявлена плагиатом идеи Волластона. Примерная конструкция:

1. Серебряная чаша заполнена ртутью. Жидкий металл обладает хорошей электропроводностью и служит подвижным контактом.
2. На дне чаши находится лепёшка воска, куда одним полюсом воткнут стержневой магнит. Второй возвышается над поверхностью ртути.
3. С высоты свисает провод, подключённый к источнику. Конец его погружен в ртуть. Второй провод — возле края чаши.
4. Если пропускать через замкнутую цепь постоянный электрический ток, провод начинает описывать по ртути круги. Центром вращения становится постоянный магнит.

Электромагнетизм

Конструкцию называют первым в мире электрическим двигателем. Но эффект электромагнитной индукции ещё не проявляется. Налицо взаимодействие двух полей, не более. Фарадей, кстати, не остановился, и сделал чашу, где провод неподвижный, а магнит двигается (образуя поверхность вращения – конус). Доказал, что нет принципиальной разницы между источниками поля. Потому индукция называется электромагнитной.

Немедленно Фарадея обвинили в плагиате и травили несколько месяцев, о чем он с горечью писал доверенным друзьям. В декабре 1821 года состоялась беседа с Волластоном, казалось, инцидент исчерпан, но… чуть позже группа учёных возобновила нападки, главой оппозиции стал сэр Хампфри Дэви. Смысл основных претензий заключался в противостоянии идее принятия Фарадея в члены Королевского общества. Это тяжким грузом давило на будущего открывателя закона электромагнитной индукции.

140. Основной закон электромагнитной индукции.

Основной
закон электромагнитной индукции гласит, что индукционный ток возникает в
проводящем контуре при всяком изменении магнитного потока, пронизывающего
поверхность, охваченную этим контуром. Однако, производя совершенно одинаковое
изменение магнитного потока в различных контурах, отличающихся только
материалом, из которого сделаны эти контуры, мы обнаружим, что в них
индуцируются токи различной силы. Изготовим, например, две катушки, совершенно
одинаковые по размерам, форме и числу витков, одну из медной проволоки, а другую
из нихромовой проволоки того же сечения и длины, и поместим их в одно и то же
магнитное поле, например внутрь длинного соленоида, одинаково ориентировав
катушки по отношению к направлению поля. Выключая магнитное поле, мы обнаружим
в обеих катушках индукционные токи, но сила тока в медной катушке будет в 70
раз больше, чем в нихромовой. Проводя разнообразные опыты подобного рода, мы
убедимся, что индукционный ток тем больше, чем меньше электрическое
сопротивление катушки, если все остальные условия опыта вполне одинаковы.

Это
обстоятельство приводит к мысли, что при неизменных условиях опыта в катушке индуцируется
определенная э. д. с., а сила тока, возникающего благодаря этому, определяется
законом Ома и поэтому оказывается обратно пропорциональной электрическому
сопротивлению цепи.

Действительно,
нетрудно осуществить простой опыт, показывающий, что для индукционных токов
закон Ома сохраняет значение. Присоединим концы катушки, в которой индуцируется
ток, к какой-нибудь цепи, сопротивление которой можно изменять, и выполним
соответствующие измерения. Включим, например, катушку I (рис. 266) в сеть
городского переменного тока, который, как известно, 100 раз в секунду изменяет
свое направление и, следовательно, 100 раз в секунду уменьшается до нуля и вновь
достигает максимального значения. Так как ток в катушке I, а значит, и его
магнитное поле непрерывно изменяются, то в катушке II будет все время
индуцироваться переменная э. д. с., направление которой также будет изменяться.
В цепь индукционной катушки II включим в качестве индикатора тока лампочку
накаливания и последовательно с ней реостат. Индукционный ток, переменный по
силе и направлению, проходя через нить лампочки, будет ее нагревать и может
довести до яркого накала. Не меняя ни катушек, ни их взаимного расположения,
увеличим сопротивление индукционной цепи в два-три раза, передвигая движок
реостата. Мы увидим, что лампочка будет светиться значительно более слабым,
красноватым накалом, что указывает на уменьшение тока, идущего через нее.

Рис. 266. При увеличении
сопротивления индукционной цепи индукционный ток уменьшается (лампочка горит
менее ярко). I – катушка с первичным током, II – катушка с индукционным током

Заменив
лампочку тепловым амперметром (§ 44), мы можем измерить силу индукционного
тока; измеряя, кроме того, полное сопротивление всей цепи, мы убедимся в том,
что и для индукционных токов справедлив закон Ома (§46):

,

где
 – сила
тока,  –
полное сопротивление цепи, т. е. сумма сопротивления индукционной катушки и
сопротивления остальных частей цепи (реостата, лампочки, амперметра и т. д.), а
через  обозначена
э. д. с. индукции, остающаяся неизменной при изменении сопротивления цепи в
наших опытах.

С
понятием э. д. с. мы встречались уже раньше при рассмотрении вопроса об
условиях возникновения и поддержания электрического тока в цепи (§ 39).
Существенное различие между случаями, рассмотренными ранее (гл. VI), и э. д. с.
индукции заключается в следующем. В случае гальванического элемента,
аккумулятора или термоэлемента мы могли установить, что э. д. с. возникает в
определенных местах цепи тока, именно, в пограничном слое между металлом и
электролитом или в месте контакта двух различных металлов. В случае же индукции
э. д. с. не сосредоточена в том или ином участке цепи, но действует во всей
индукционной цепи в целом, т. е. во всех точках цепи, где изменяется поток
магнитной индукции.

В
случае витка, охватывающего линии поля, э. д. с. возникает во всех точках витка
и может быть подсчитана для витка в целом. В случае нескольких витков то же
происходит в каждом из них: э. д. с. катушки складывается из э. д. с. отдельных
витков.

Формулировка Фарадея

Р

(21)

ассмотрим
случай движения проводника в равномерном
неподвижном магнитном поле (рис. 11).
Вектор индукции в магнитного поля
параллелен плоскости рисунка, проводник
расположен перпендикулярно к плоскости
рисунка и движется со скоростьюv,
пересекая силовые линии неподвижного
магнитного поля под угломα. В
результате пересечения магнитных
силовых линий в проводнике индуктируется
э.д.с.

В соответствии с равенством (21) закон
электромагнитной индукции по Фарадеюформулируется следующим образом:

э.д.с. е, индуктированная
в проводнике, движущемся в неподвижном
поле, прямо пропорциональна индукции
магнитного поля В, длине
проводника l,
скорости проводника v
и синуса угла α между векторами
индукции и скорости.

Можно
упрощенно так сформулировать этот
закон:э.д.с. – это количество магнитных
силовых линий, пересеченных проводником
в единицу времени, считая, что точное
вычисление самой э.д.с. проводится по
формуле (21),

где е– э.д.с. в вольтах (В);

В– индукция магнитного поля в
тесла (Тл);

l– длина проводника
в метрах (м);

v– скорость в метрах
в секунду (м/с).

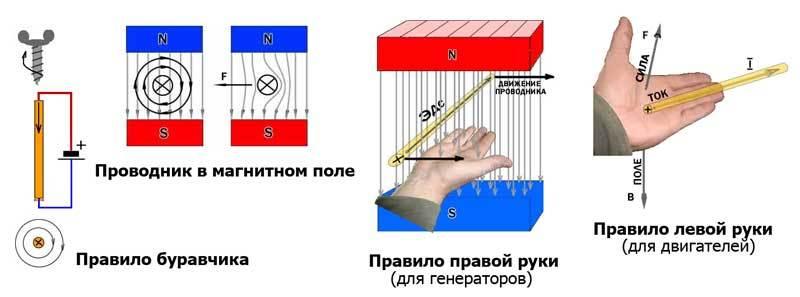
Направлениеиндуктированной э.д.с.еопределяетсяпо правилу правой
руки.

На рисунке 12 проводник
движется в неподвижном равномерном
магнитном поле постоянных магнитов
(электромагнитов), пересекая силовые
линии под прямым углом (α = 90°). Согласно
правилу правой руки необходимо:
расположить
ладонь правой руки перпендикулярно к
линиям вектора магнитной индукции
В
так, чтобы
линии входили в ладонь, а отставленный
в сторону большой палец направить по
движению проводника, тогда вытянутые
пальцы будут показывать направление
индуктированной э.д.с. е.
Показанное на рисунке 11 направление
э.д.с. (крестик) тоже соответствует этому
правилу.

Магнитное поле и магнетизм

Магнитная индукция гораздо точнее описывает поле, нежели прочие методы. Запутанные термины мешают пониманию. Индукцию путают с напряженностью. Оба термина векторные, описывают поле. Напряженность не зависит от характеристик среды, отличаясь этим. Магнетизм известен издревле. Ученые бессильны точно назвать дату начала применения поля Земли для навигации моряками, историки выявили следующие любопытные факты:

1. Ольмеки (древнее индейское племя) применяли намагниченные иглы за 1500 лет до н.э. Отсутствуют точные свидетельства, касающиеся назначения конструкции. Полагают, пользуясь магнетизмом древний народ определял направление.
2. В Китае первые письменные упоминания касаются II века до н.э. Магнитные иглы использовались для предсказаний по характеру рельефа земной поверхности, в целях обустройства жилищ по методикам Фэн-Шуй.

Исторические факты заставляют называть первой современной цивилизацией, начавшей практиковать навигацию с ориентацией магнитным полем Земли, Китай. X – XI век нашей эры. Конструкция тщательно замалчивается письменными источниками. Рискнем предположить, компас повторял наработки прорицателей:

• Конец металлической иглы намагничивается железняком.
• Изделие подвешивается на шелковой нити, фиксатором точки крепления выступает воск.

Приспособления, изготовленные таким образом, смотрят то на юг, то на север. В зависимости от условий намагничивания иглы. Европы узнала компас несколькими веками позже. Первым источником, описывающим конструкцию подобных приборов, наравне с астролябией, является простое письмо (1269 год н.э.), набросанное Петрусом «Перегринусом» (Пилигримом) некоему землевладельцу в дни осады итальянской Лучеры. По-видимому, прозвище автора указывает, что автор хорошо знаком с темой. Астролябия помогала определить местное время, в сочетании с компасом становилось возможным произвести вычислении географических координат. Оба прибора несказанно упрощали навигацию (разумеется, приоритет отдается морским путешествиям).

Существовал минус: для каждой широты следовало изготовить карту на тимпане (вращающаяся вкладка корпуса астролябии). Мореход, применяя нужный диск, решал задачу на любых широтах. Разумеется, должен заранее позаботиться обзавестись нужными картами тимпанов. Иначе измерения становились неточными, некорректными. Видите, сколько пришлось пережить трудностей путешественникам, вернемся к магнитному полю Земли. Явление описывает индукция. Ходили слухи: Тесла использовал знания о величине магнитного поля Земли, выбирая параметры электрических приборов. Впрочем, попахивает фантазий, пришельцами со звезд, Второй мировой войной.

Индукция у магнитного поля Земли присутствует, каждый желающий найдет электронную карту, возникни потребность. Магнитные полюса не совпадают с истинными. Карта магнитной индукции будет иметь меридианы, отличающиеся от пространственных. На средних широтах не мешает мореплавателям ориентироваться, пользуясь компасом.

II. Примеры решения задач

Пример 5.1.Короткозамкнутый виток провода
сопротивлением R, имеющий форму квадрата
со стороной а, поместили в однородное
магнитное поле с индукцией В,
перпендикулярной плоскости витка. Затем
витку придали форму половины окружности
(не растягивая провод, а только деформируя
его). Какой заряд протечет через поперечное
сечение провода в результате такой
деформации.

Решение.

Из закона электромагнитной
индукции:

,

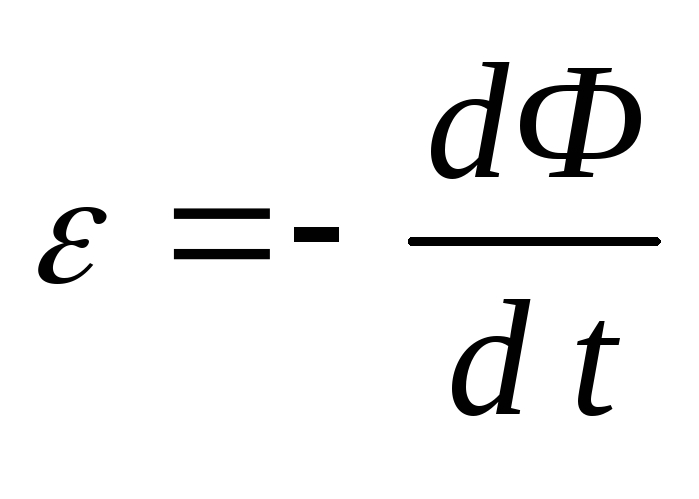где магнитный поток
,
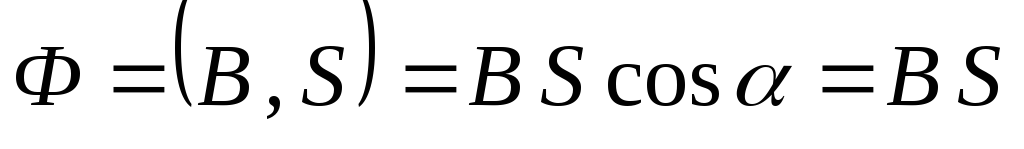т.к. магнитное поле перпендикулярно
плоскости витка, т.е. угол между вектором
магнитной индукции и нормалью к плоскости
витка равен нулю.

Из закона Ома,

где R – сопротивление
контура. Тогда:

Начальная площадь
контура:
,
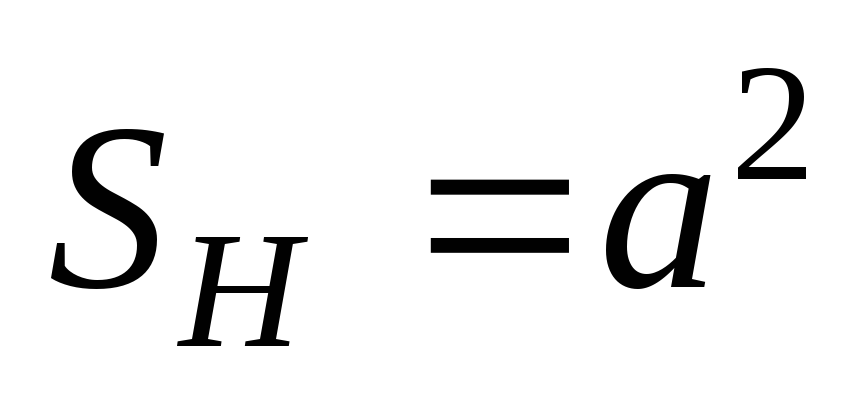конечная площадь контура – площадь
половины окружности:,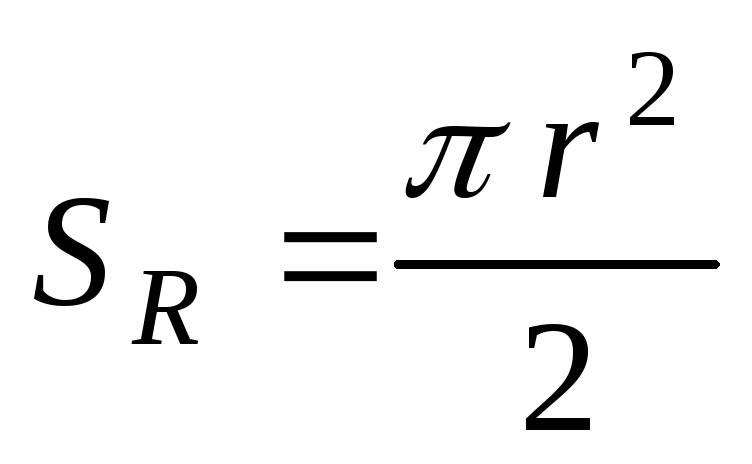
где r – радиус окружности. Радиус
окружности найдем из условия, что длина
провода остается неизменной:.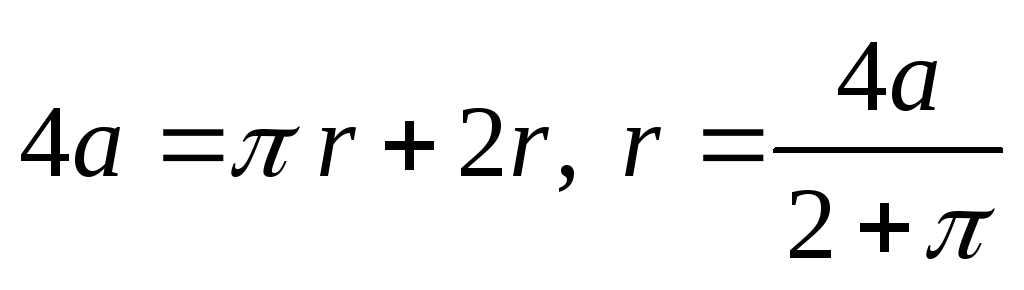
Тогда конечная площадь контура:.

Таким образом, заряд
который пройдет через поперечное сечение
провода:

.

Пример 5.2.Кольцо радиуса r вращается вокруг оси
лежащей в его плоскости, так что угловая
скорость зависит от времени по закону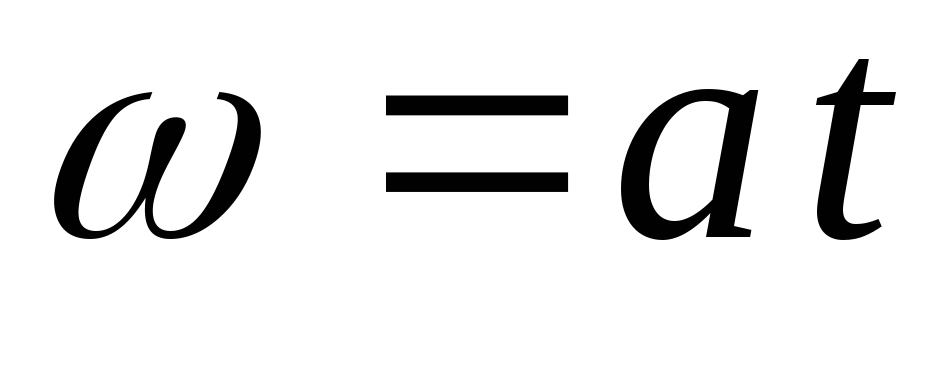(где а > 0). Кольцо помещено в однородное
магнитное поле с индукцией В, направленной
перпендикулярно к оси вращения. Найти
индукционный ток в кольце, если его
сопротивление R.

Решение.

Индукционный ток :

.

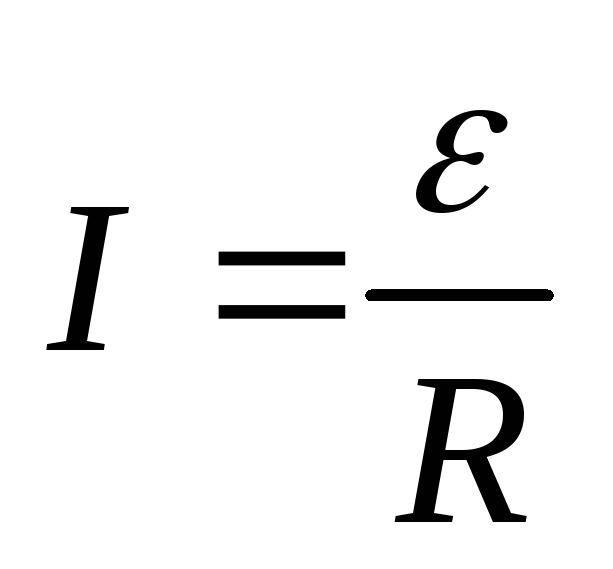Из закона электромагнитной
индукции:

,

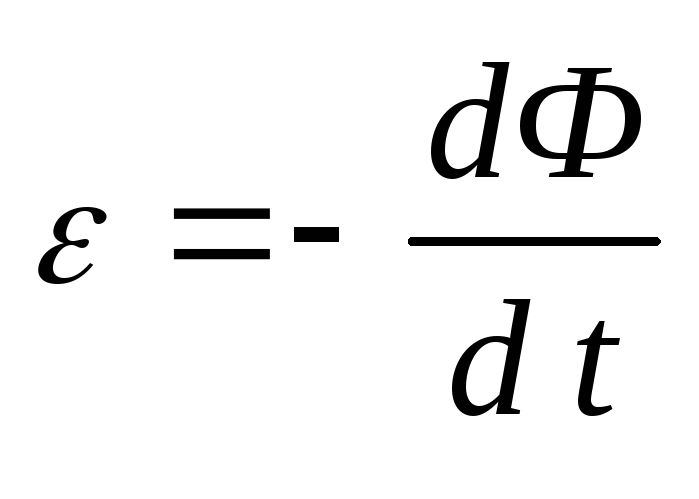где магнитный поток
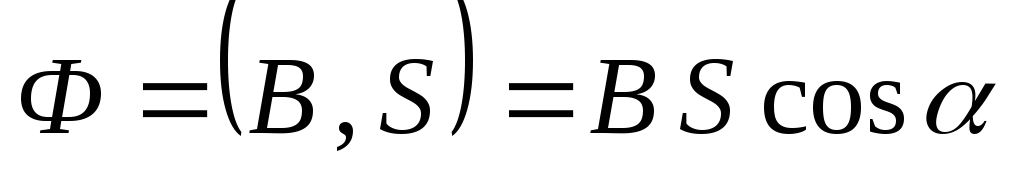,— угол между
вектором магнитной индукции и нормалью
к плоскости контура. Тогда:

.

В начальный момент
времени нормаль к контуру совпадает с
направлением вектора индукции магнитного
поля:

.

В момент времени
,
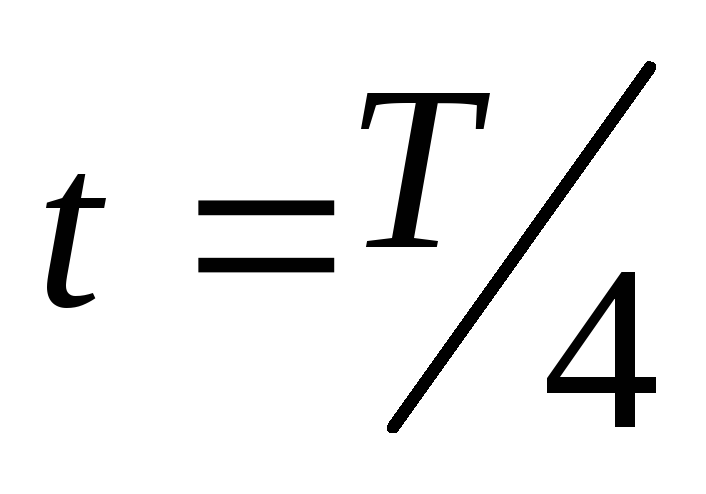(гдеТ– период вращения, т.е. время
одного полного оборота) кольцо повернется
на угол 90вокруг
своей оси, т.е.= 90и магнитный поток
равен нулю.

В момент
времени
,
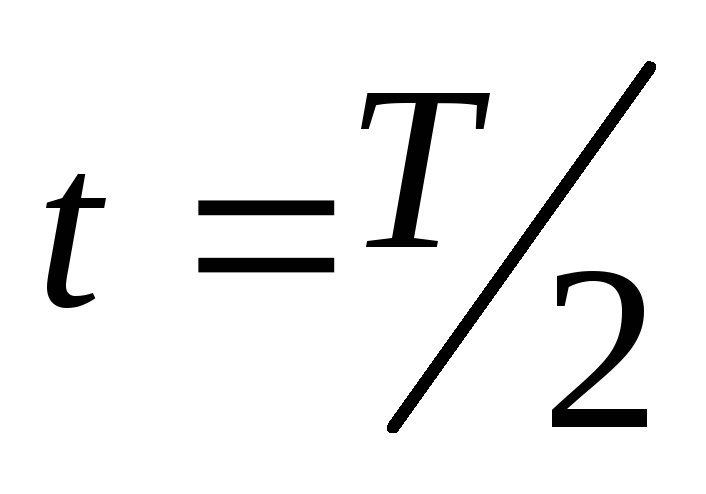кольцо повернется на угол 180вокруг своей оси, т.е.= 180и магнитный
поток равен:

.

В момент
времени
,
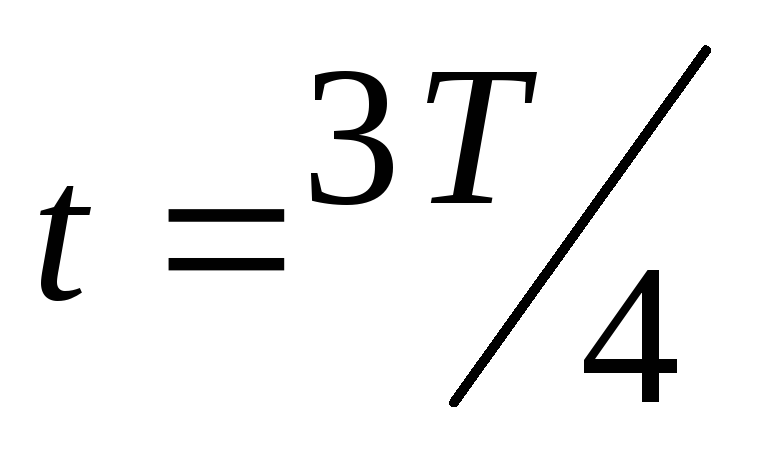кольцо повернется на угол 270вокруг своей оси и= 270, т.е. магнитный
поток равен нулю.

Таким
образом, зависимость магнитного потока
от времени имеет вид:,
где.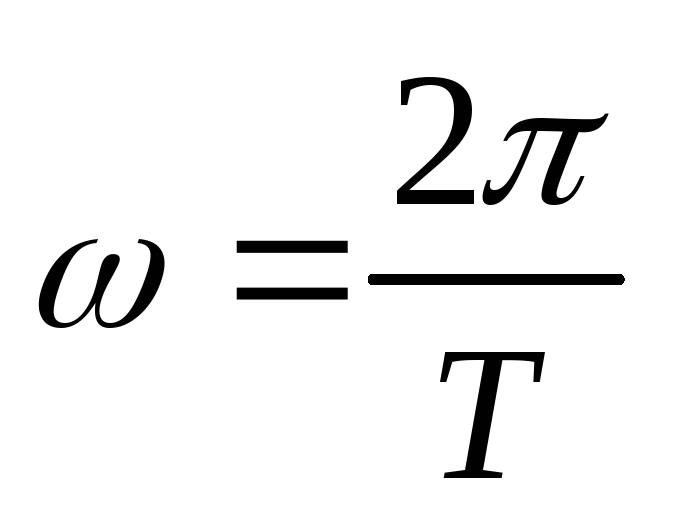

Магнитный поток:
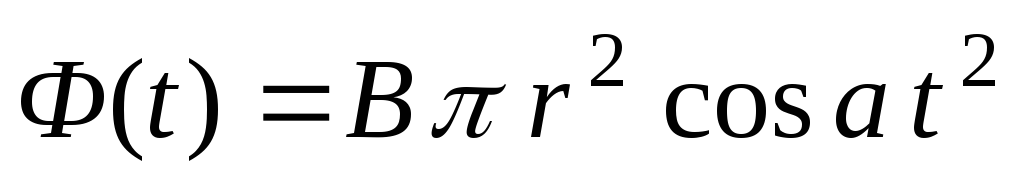и.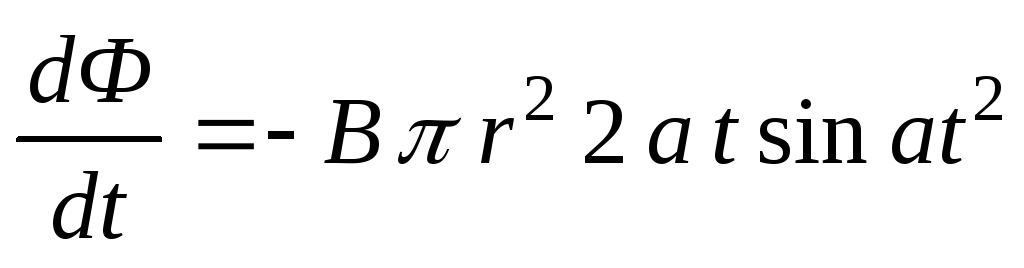
Тогда индукционный ток равен:

.

Пример 5.3.В очень длинном соленоиде, радиус
которого равенR, а число витков на
единицу длины равноn, ток изменяется
со временем по закону: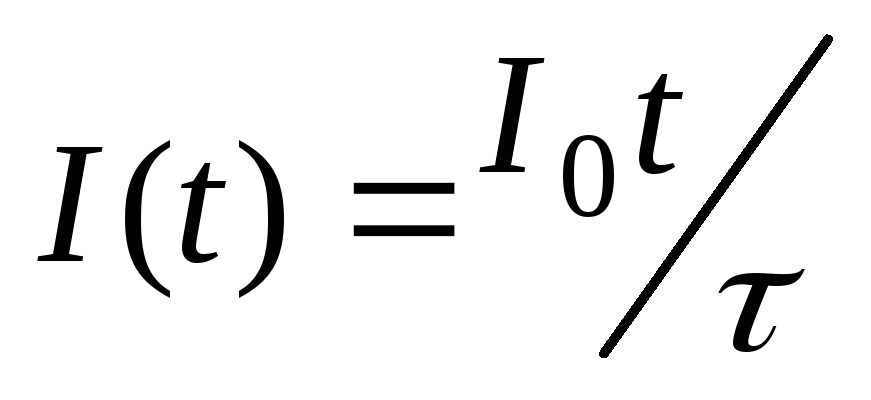(гдеIи— положительные постоянные). Определит
напряженность электрического вихревого
поляЕ(r)(внутри и снаружи соленоида)
в любой момент времени.

Решение.

Закон электромагнитной
индукции:

,

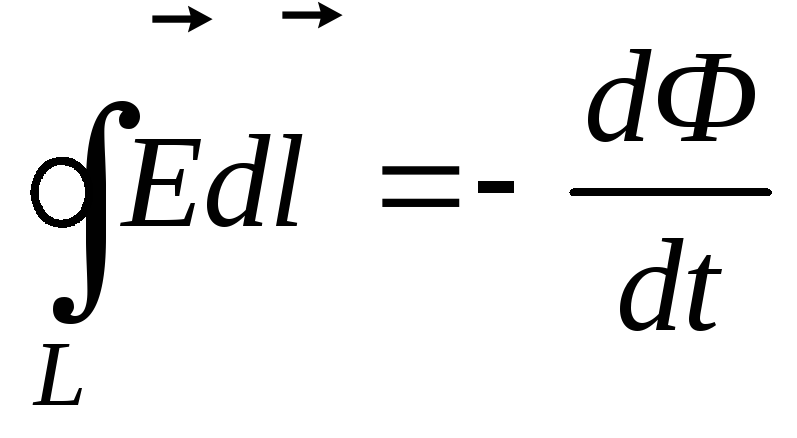где
— поток вектора магнитной индукции.
Индукция магнитного поля внутри
соленоида:,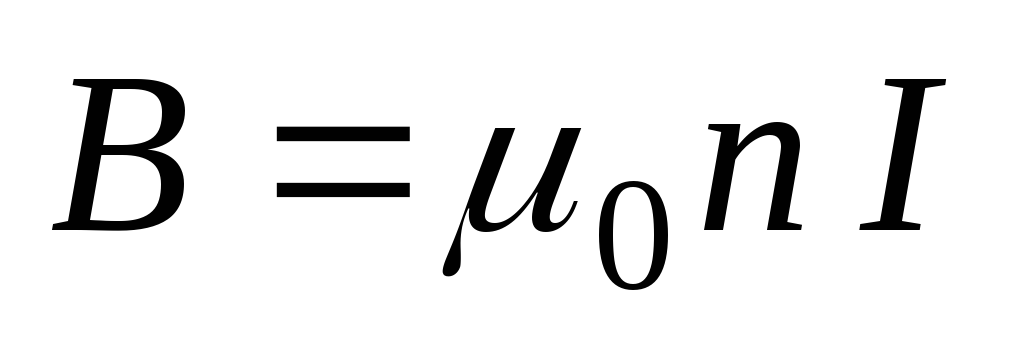
индукция магнитного поля вне бесконечного
соленоида равна нулю. Силовые линии
магнитного поля параллельны оси
соленоида, силовые линии электрического
поля – окружности, плоскости которых
перпендикулярны оси соленоида. Выбираем
замкнутый контур вдоль силовой линии
электрического поля внутри соленоида,
тогда поток вектора магнитной индукции
через поверхность ограниченную данным
контуром равен:

,

где r– радиус
замкнутого контура.

.

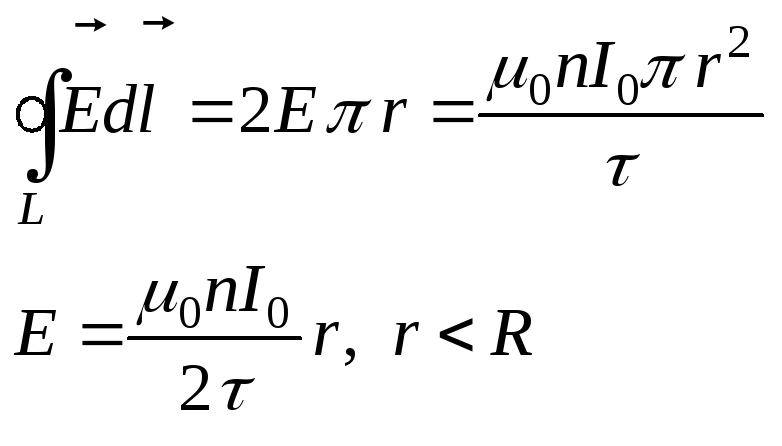
Если замкнутый контур
выбираем вне соленоида, то
.

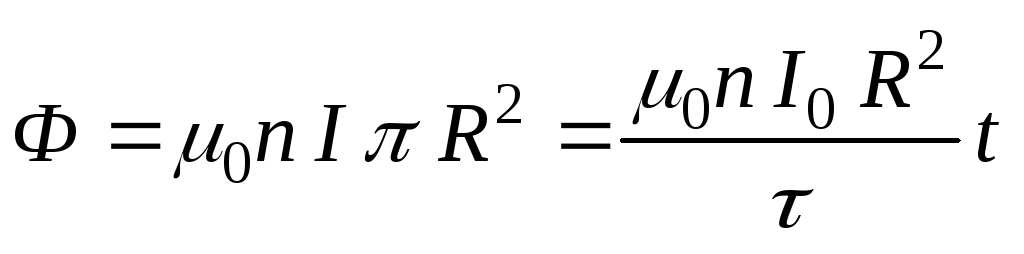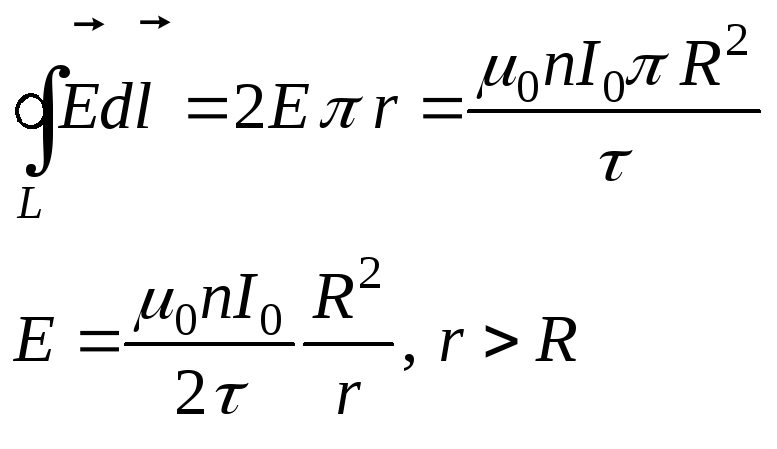
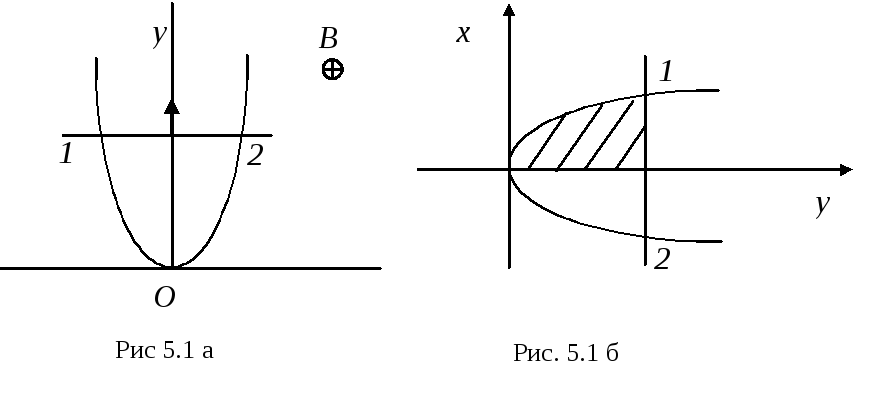
Пример 5.4.Провод, имеющий форму параболы,
находится в однородном магнитном поле
с индукциейВ. Из вершины параболы
в момент времениt= 0 начали перемещать
перемычку 12 (рис. 5.1 а). Найти э.д.с. в
образовавшемся контуре как функциюу,
если перемычку перемещают с постоянным
ускорениема, причем в моментt= 0 скорость перемычки была равна нулю.

Решение.

Из закона электромагнитной
индукции:

,

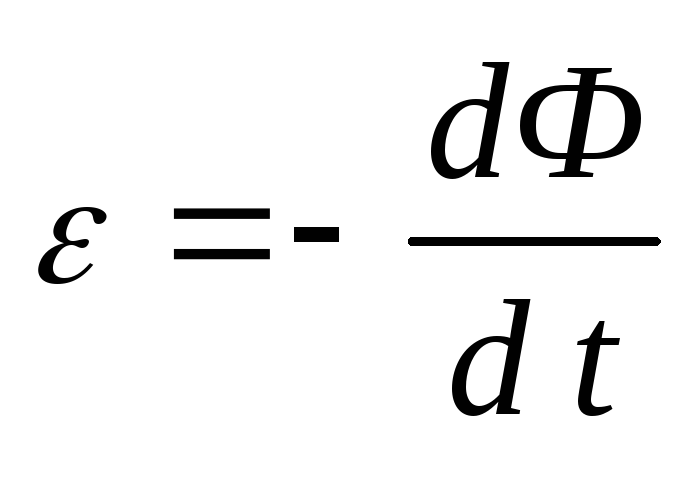где магнитный поток
,= 0 — угол между
вектором магнитной индукции и нормалью
к плоскости контура.

Чтобы найти площадь
S, вычислим площадь заштрихованной
фигурыSна
рис. 5.1 б,
учитывая, что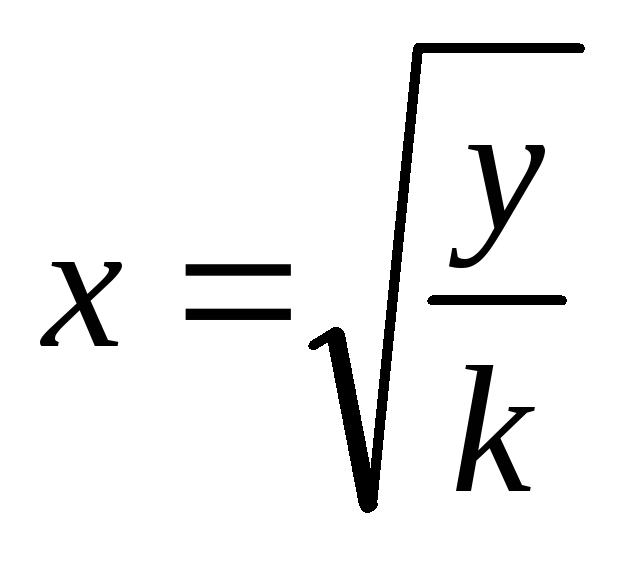и.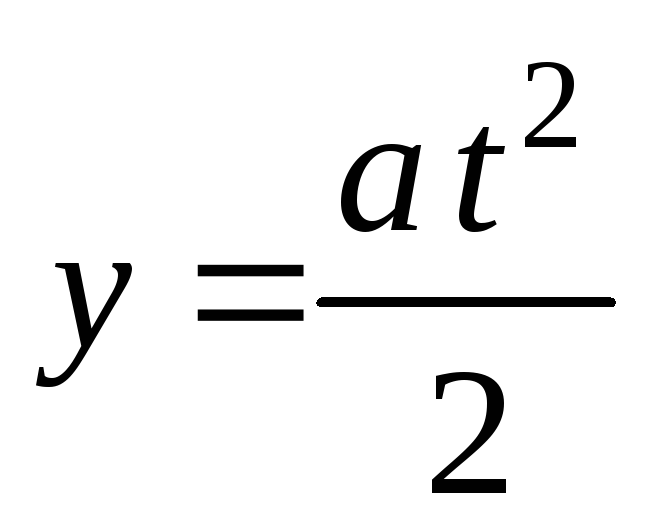

.

.

.

.

Пример 5.5.По П-образному проводнику, расположенному
в горизонтальной плоскости, может
скользить без трения перемычка 12 (рис.
5.2). Перемычка имеет длинуl, массуmи сопротивлениеR. Вся система
находится в однородном магнитном поле
с индукциейВ. В момент времениt= 0 на перемычку стали действовать
постоянной горизонтальной силойF,
и перемычка начала перемещаться вправо.
Найти зависимость от времени скорости
перемычки. Самоиндукция и сопротивление
П-образного проводника малы.

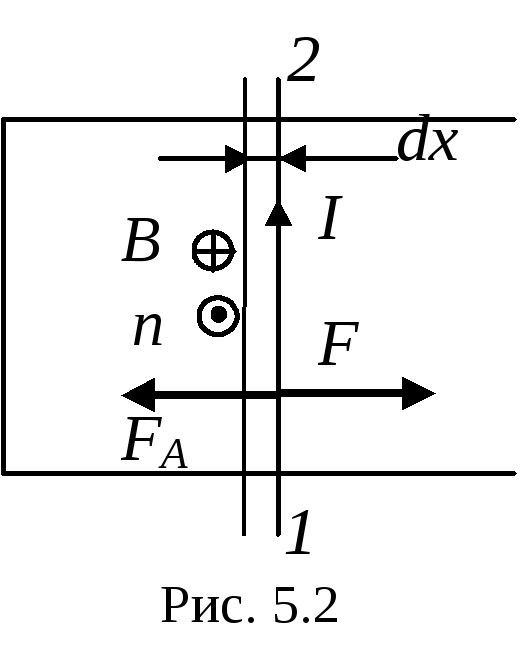
Решение.

При перемещении
перемычки под действием силы Fв контуре возникает ЭДС индукции и
индукционный ток (направление тока
указано на рис. 5.2):

,

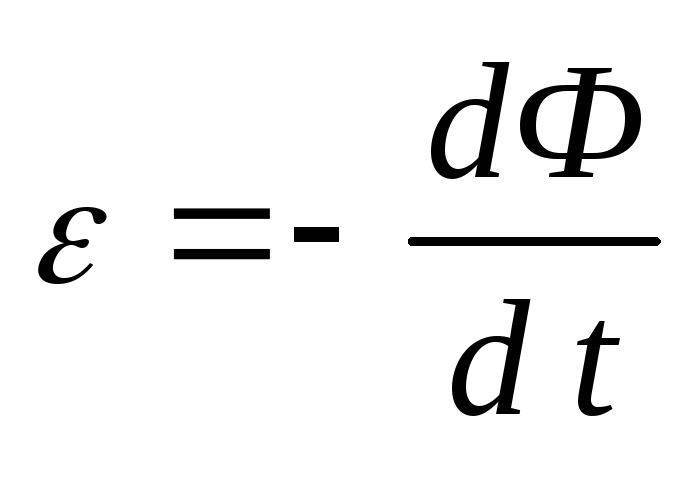где магнитный поток
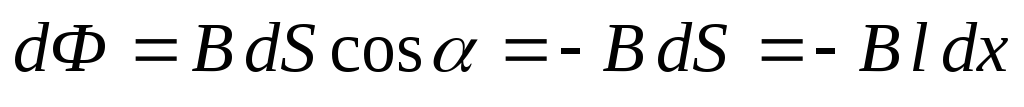,= 180 — угол между
вектором магнитной индукции и нормалью
к плоскости контура. Величина индукционного
тока определяется выражением:

,

где v– скорость движения перемычки.

На проводник, по
которому течет ток, в магнитном поле
действует сила Ампера:

.

Уравнение движения
перемычки имеет вид:

Решаем дифференциальное
уравнение:

.

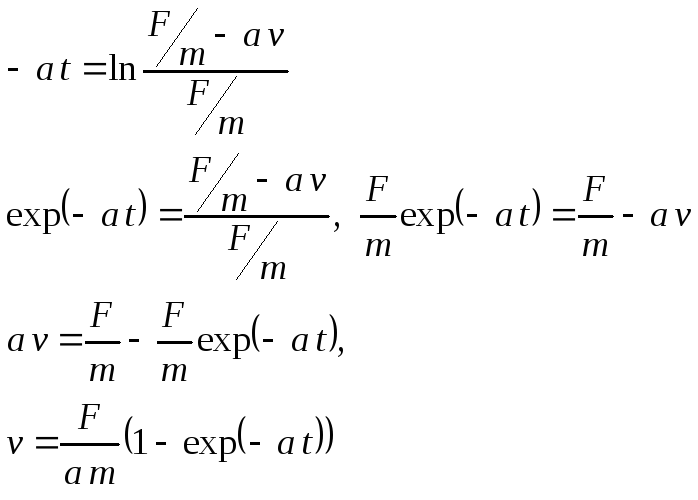
97. Закон электромагнитной индукции

Выяснив условия и причины возникновения э. д. с. индукции, выведем теперь формулу дли ее вычисления. В магнитном поле расположен контур abcd, одна из сторон которого cd сделана подвижной (рис. 146). Будем перемещать ее вправо. При этом магнитный поток, проходящий через площадь контура, начнет изменяться. На концах подвижной стороны рамки возникнет э. д. с. индукции (на остальных неподвижных частях рамки она не возникнет). Наведенная э. д. с. вызовет ток в рамке. По правилу правой руки этот ток в подвижной стороне рамки направлен от нас.

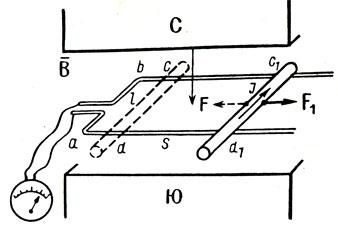Рис. 146. К выводу формулы закона электромагнитной индукции

На сторону cd, длина которой l, действует сила Ампера F = BIl. Определив ее направление по правилу левой руки, видим, что она направлена против скорости движения проводника cd. Чтобы индукционный ток не прекращался и был постоянным по. величине, необходимо подвижную сторону контура перемещать равномерно, т. е. действовать на нее с силой F₁ = F. При перемещении проводника cd на пути s внешняя сила F₁ совершает работу A₁ =F₁s. Заменив F₁, получим

A₁ = BIls. (1)

В этой формуле ls = ΔS есть изменение площади контура. Значит, A₁ = BIΔS, где BΔS = ΔФ (изменению магнитного потока за время Δt, пока движется подвижная сторона рамки). Тогда

А₁ = IΔФ.

Образовавшийся в контуре ток обладает энергией, которая равна работе по перемещению q кулонов по всей цепи:

A₂ = q(U + u), где U + u = E; q = IΔt. Тогда

A₂ = EIΔt. (2)

Согласно закону сохранения энергии, A₁ + A₂ = 0. Или IΔФ + EIΔt = 0. Отсюда э. д. с. индукции

Изменение магнитного потока за единицу времени есть средняя скорость изменения магнитного потока. Чем меньше Δt, тем меньше средняя э. д. с. Е будет отличаться от ее мгновенного значения. Следовательно, электродвижущая сила индукции прямо пропорциональна скорости изменения магнитного потока. Этот вывод называется законом электромагнитной индукции. Э. д. с. индукции зависит от скорости изменения магнитного потока, а не от его величины.

При выводе последней формулы мы имели контур, состоящий из одного витка. В случае, когда «индукционный ток возникает в катушке, имеющей n витков, соединенных последовательно, каждый из которых пронизывается магнитным потоком ΔФ, э. д. с. индукции будет в n раз больше. Знак минус в формуле закона электромагнитной индукции выражает математически правило Ленца: магнитное поле индукционного тока препятствует изменению магнитного потока, который вызвал этот ток.

Задача 34. Катушка диаметром 5 см, состоящая из 100 витков, расположена в магнитном поле с индукцией 2 тл так, что ее ось параллельна линиям индукции (рис. 147, а) и поворачивается на 180° в течение 0,4 сек (рис. 147, б). Определить среднее значение э. д. с. индукции, возникшей в катушке.

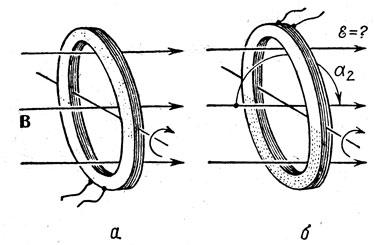Рис. 147. К задаче 34

Тогда ΔФ = -BS — (+BS) = -2 BS. Площадь сечения катушки S = πd2/₄, значит, Ф = -2 В πd2n/₄. Следовательно,

Вычислим

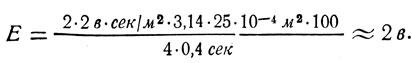
Отв.: E ≈ 2 в.

История открытия

Явление электромагнитной индукции было открыто сразу двумя учеными. Это были Майкл Фарадей и Джозеф Генри, сделавшие свое открытие в 1831 году. Публикация Фарадеем результатов проведенных экспериментов была сделана раньше его коллеги, поэтому индукцию связывают именно с этим ученым. В дальнейшем это понятие было включено в систему СГС.

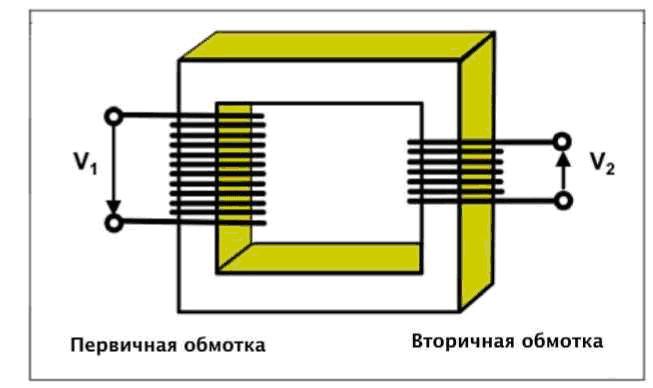
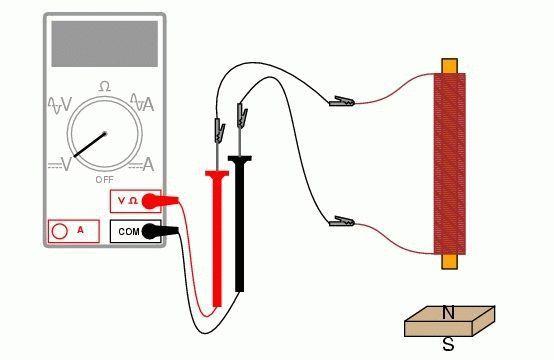
Для демонстрации явления использовался железный тор, напоминающий конфигурацию современного трансформатора. Противоположные стороны его были обмотаны двумя проводниками с целью использования электромагнитных свойств.

К одному из проводов подключался ток, вызывающий своеобразную электрическую волну при прохождении сквозь тор, и некоторый электрический всплеск с противоположной стороны. Наличие тока было зафиксировано гальванометром. Точно такой же всплеск электричества наблюдался и в момент отключения провода.

Постепенно были обнаружены и другие формы проявления электромагнитной индукции. Кратковременное возникновение тока наблюдалось во время генерации его на медном диске, вращающемся возле магнита. На самом диске был установлен скользящий электропровод.

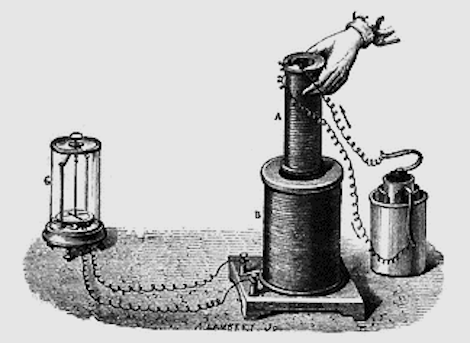
Наибольшие представление о том, что такое индуктивность, дал эксперимент с двумя катушками. Одна из них, с меньшими размерами, подключена к жидкостной батарее, расположенной на рисунке с правой стороны. Таким образом, через эту катушку начинает протекать электрический ток, под действием которого возникает магнитное поле.

Когда обе катушки находятся в неподвижном положении относительно друг друга, никаких явлений не происходит. Когда небольшая катушка начинает двигаться, то есть выходить из большой катушки или входить в нее, наступает изменение магнитного потока. В результате, в большой катушке наблюдается появление электродвижущей силы.

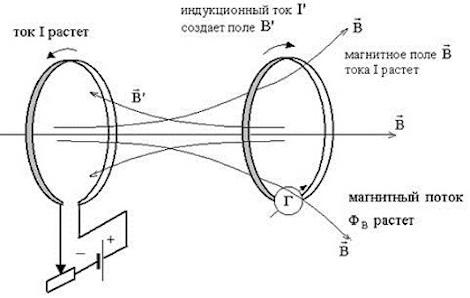
Открытие Фарадея доработал другой ученый – Максвелл, который обосновал его математически, отображая данное физическое явление дифференциальными уравнениями. Еще одному ученому-физику – Ленцу удалось определить направление электротока и ЭДС, полученных под действием электромагнитной индукции.

Обоснование метода измерений

Индукционный
метод определения величины магнитной
индукции В
на оси кругового тока заключается в
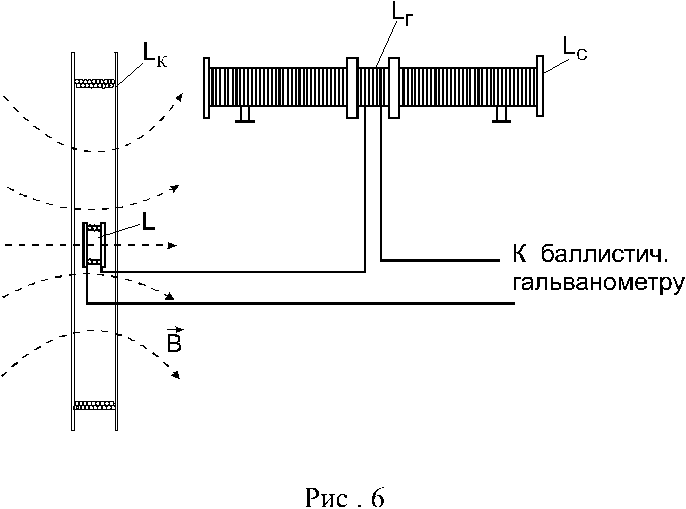
следующем. На оси кругового тока,
создаваемого катушкой L_K
(рис.6), располагают небольшую плоскую
катушку L,
имеющую N₁витков и
площадь одного витка S₁,которая
замкнута на баллистический гальванометр.
При изменении направления тока в круговом
витке L_Kна
противоположное , магнитный поток через
Lизменяется
от –Ф до +Ф. В катушке L
возникает ЭДС индукции, и в цепи
гальванометра – индукционный ток. При
этом заряд q
, протекший
по

баллистическому
гальванометру, оказывается пропорциональным
значению В
в том месте поля, где располагается
измерительная катушка L.
На основании (20) и (21) можно записать:

(2N₁S₁/R₂)B
= b‘
m ,
(22)

где
R₂
– сопротивление цепи баллистического
гальванометра.

Из (22) следует:

B
= (R₂/2N₁S₁)
b‘
m = A₂b‘
m
(23)

Величины
R₂,
N₁,
S ₁входящие
в А₂,
остаются неизменными параметрами цепи
гальванометра, которые могут быть
измерены при изготовлении установки.

Равенство
(23) позволяет определить В,
измерив отброс «
m » зайчика
гальванометра при коммутации тока,
создающего исследуемое магнитное поле,
и определив заранее b‘.

Баллистическую
постоянную b‘
установки определяют, используя известное
магнитное поле, или поле, магнитная
индукция которого сравнительно легко
и достаточно точно может быть рассчитана.
Таким полем может быть поле внутри
«бесконечного соленоида» L_C, представляющего
собой катушку, длина которой (намотанной
части катушки) в несколько раз больше
диаметра ее витка. Для проведения
измерений на бесконечный соленоид L_Cнадевают
катушку L_Г,
включенную в цепь гальванометра Г
последовательно с подвижной катушкой
L.
При изменении направления тока в
соленоиде L_Cна противоположное
, в катушке L_Гсоздается
эдс индукции и гальванометр фиксирует
отброс m_с.
На основании (22) можно записать:

(2NS/R₂
) В_C
=
b‘m_с
, (24)

где
N
-число витков катушки L_Г,,
S — площадь
ее витка, R₂— сопротивление
цепи гальванометра, В_с— магнитная
индукция на оси соленоида L_c.

Величина
В_с
определяется:

B_c=mmi_C
n
, (25)

где
i_C
— ток по соленоиду L_C,
n
— количество витков приходящихся на
единицу длины намотки соденоида .

На основании (24) и (25) имеем: (2NSmmi_Cn)/R₂
=b’m_C

откуда

b
‘=(2mm_CnNS
i_C
)/R₂
m_C=A₁
i_C
m_C

(26)

Величины,
входящие в А₁,
являются неизменными параметрами
используемой установки. Значения А₁
и А₂
указаны около рабочей панели.

Используя
бесконечный соленоид, измерив его ток
i_C
и отброс m_C
зайчика гальванометра при коммутации
тока i_C, можно
определить значение баллистической
постоянной b‘.

Величину магнитного потока Фчерез измерительную подвижную катушкуLможно определить, воспользовавшись
(22):

Ф
= N₁S₁B
= (R₂/2)
b‘
m
(27)

История Майкла Фарадея

Майкла Фарадея забрали из школы вместе со старшим братом, послужил поводом – дефект речи. Первооткрыватель электромагнитной индукции картавил, раздражая учительницу. Та дала денег, дабы купили палку и высекли потенциального клиента логопеда. Причём старшему брату Майкла.

Будущий светило науки был поистине любимцем судьбы. На протяжённости жизненного пути он, при должной настойчивости, находил помощь. Брат с презрением вернул монету, сообщив об инциденте матери. Семья не считалась богатой, и отец, талантливый ремесленник, с трудом сводил концы с концами. Братья рано стали искать работу: семья жила на милостыню с 1801 года, Майклу в ту пору шёл десятый год.

С тринадцати Фарадей поступает в книжную лавку разносчиком газет. Через весь город едва-едва успевает по адресам на противоположных концах Лондона. Ввиду прилежности хозяин Рибо дарует Фарадею место ученика переплётчика на семь лет бесплатно. В давнюю пору человек с улицы платил мастеру за процесс приобретения ремесла. Как и Георгу Ому умение механика, Фарадею в будущем процесс переплётного дела пригодился в полной мере. Большую роль сыграл факт, что Майкл скрупулёзно читал книги, попадающие к нему в работу.

Майкл Фарадей

Фарадей пишет, что одинаково охотно верил трактату миссис Марсет (Беседы о химии) и сказкам Тысячи и одной ночи. Желание стать учёным сыграло в этом деле важную роль. Фарадей избирает два направления: электричество и химию. В первом случае основным источником знаний служит Британская энциклопедия. Пытливый ум требует подтверждения написанного, юный переплётчик постоянно проверяет знания на практике. Фарадей становится опытным экспериментатором, что сыграет ведущую роль при исследовании электромагнитной индукции.

Напомним, что речь идёт об ученике без собственного дохода. Старший брат и отец посильно оказывали помощь. Начиная с химических реактивов и заканчивая сборкой электростатического генератора: для опытов нужен источник энергии. Одновременно Фарадей умудряется посещать платные лекции естествознания и скрупулёзно заносит знания в блокнот. Потом переплетает заметки, пользуясь приобретёнными навыками. Срок ученичества заканчивается в 1812 году, Фарадей начинает искать работу. Новый хозяин не столь покладист, и, несмотря на перспективу сделаться наследником дела, Майкл на пути к открытию электромагнитной индукции.

Научный путь Фарадея

В 1813 году судьба улыбается учёному, давшему миру представление об электромагнитной индукции: удаётся попасть на место секретаря к сэру Хампфри Дэви, недолгий период знакомства в будущем сыграет роль. Фарадею невыносимо исполнять долее обязанности переплётчика, он пишет письмо Джозефу Бэнксу, тогдашнему президенту Королевского научного общества. О характере деятельности организации расскажет факт: Фарадей получил место, называемое старший прислужник: помогает лекторам, вытирает пыль с оборудования, следит за транспортировкой. Джозеф Бэнкс игнорирует послание, Майкл не унывает и пишет Дэви. Ведь прочих научных организаций нет в Англии!

Хампфри Дэви

Дэви относится с большим вниманием, поскольку лично знаком с Майклом. Не будучи одарён от природы умением говорить – вспомним про школьный опыт – и излагать мысли письменно, Фарадей берет специальные уроки для развития необходимых навыков

Опыты тщательно систематизирует в блокноте, мысли излагает в кружке друзей и единомышленников. К моменту знакомства с сэром Хампфри Дэви достигает недюжинного мастерства, тот ходатайствует о принятии новоиспечённого учёного на вышеупомянутую должность. Фарадей рад, а изначально фигурировала идея назначить будущего гения мыть посуду…

По воле рока Майкл вынужден слушать лекции на разные темы. Помощь профессорам требовалась лишь периодически, в остальном допускалось находиться в аудитории и слушать. Учитывая, сколько стоит образование в Гарварде, это стало неплохим досугом. Через полгода блестящей работы (октябрь 1813 года) Дэви приглашает Фарадея в путешествие по Европе, война окончена, нужно оглядеться. Это стало хорошей школой первооткрывателю электромагнитной индукции.

По возвращении в Англию (1816 год), Фарадей получает звание лаборанта и публикует первую работу по исследованию известняка.

B и H магнитная индукция

Магнитная индукция B измеряется теслами (СИ), Тл эквивалентно Н с / Кл м. Н – ньютон, единица измерения силы; с – секунда времени; Кл – кулон, электрический заряд; м – метр расстояния. СГС для тех же целей применяет гауссы (Гс = √г / с √см), г – грамм массы; с – секунда времени; см – сантиметр расстояния. H магнитная индукция измеряется амперами на метр (СИ) или эрстедах (СГС). Русскоязычная литература именует Н напряженностью поля.

Единица тесла введена в 1960 году Международной конференцией по весам и мерам в честь скончавшегося Николы Тесла. Фактически с начала существования СИ. Как ученые жили до этого? К 1948 году зародилась идея внедрения СИ, уже существовала СГС. Истоки последней заложены в 1832 году Карлом Фридрихом Гауссом, искавшим единый базис для отраслей физики, дабы проще было связать разнородные законы. Ученый задался тремся основными единицами: миллиметр, миллиграмм, секунда.

Гаусс скончался вскоре после введения понятия магнитная индукция и деления величины на В и Н, однако в 1874 году Джеймс Максвелл, лорд Кельвин дополнили перечень новыми величинами. Магнитную индукцию назвали в честь основателя, одновременно систему нарекли СГС (до этого именовалась гауссовой). Что касается СИ, теслу можно представить через базовые или производные единицы разным образом. Вебер, отнесенный на квадратный метр.

Отталкивание катушек с током

В вакууме два вида индукции (Н и В) связаны через постоянные. Чтобы отличить одно от другого, Н именуется вектором напряженности магнитного поля. Понятно, что смыслом не сильно отличается от В. В формуле:

1. μ – магнитная проницаемость среды.
2. μ0 – магнитная постоянная (проницаемость вакуума). В системе СГС равна 1, в вакууме В и Н одинаковы. В СИ составляет 1,257 микроньютона на квадратный ампер.

Постоянные введены специально, чтобы связать Н и В — характеристики магнитного поля. Кстати, существует множество версий, почему лорд Кельвин назвал векторы таким образом (литеры Н и В). Интересующимся рекомендуем ознакомиться с понятиями: относительная магнитная проницаемость (отношение абсолютной μ к постоянной μ0), магнитная восприимчивость (относительная магнитная проницаемость, увеличенная на 1). Поможет лучше понять формулы литературных источников, где зависимость между В и Н иного вида приведенного обзором.

Можете найти множество законов, формул, касающихся магнитной индукции, показывающих, сколь важное место занимает параметр в теории. Авторам неизвестно, пользовался ли подобными величинами Никола Тесла при разработке многофазного асинхронного двигателя, но неспроста же величине дали имя великого ученого!